Window Function Options for DFT of Harmonic Forces

Window function options for Discrete Fourier Transform (DFT) of harmonic forces are available for Maxwell 2D and 3D transient solvers and support both rotational and non-rotational models.

The Discrete Fourier Transform (DFT) operates on a finite-length time sequence to compute its spectrum. For a continuous signal like a sine wave, you need to capture a segment of the signal in order to perform the DFT. Usually, you also need to apply a window function to the captured signal before taking the DFT. A window function (also known as an apodization function or tapering function) is a mathematical function that is zero-valued outside of some chosen interval, normally symmetric around the middle of the interval, usually near a maximum in the middle, and usually tapering away from the middle. The mismatch in amplitude between the two ends of the signal distorts the spectrum, a phenomenon called spectral leakage. Spectral leakage can be caused by discontinuities in the non-integer number of periods in sampled signals that usually happen in asynchronous machines. This can be improved using windowing. Maxwell provides several window functions for the DFT of harmonic forces. These include

• Rectangular (default)

• Triangular

• Van Hann

• Hamming

• Blackman

• Lanczos

• Welch

Refer to FFT Window Functions for detailed information on each of these window function types.

To select the various window function options:

1. Either select Maxwell 2D (or Maxwell 3D) > Enable Harmonic Force Calculation, or right-click on the design in the Project Manager tree and select Enable Harmonic Force Calculation to open the Enable Harmonic Force Dialog box.

2. Specify the Window function type using the drop-down menu on the Advanced tab.

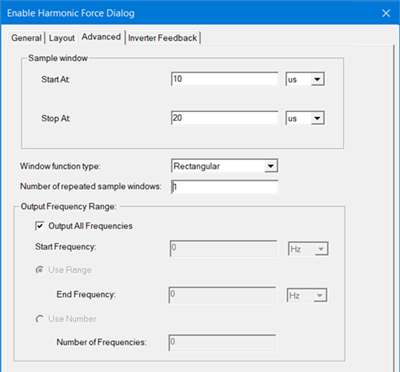
   Non-Rotational Setup

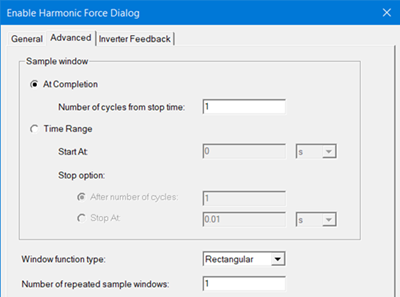
   Rotational Setup