Vector Potential

The Vector Potential boundary is available for use in Magnetostatic, Eddy Current, and Transient solver type designs. Use Vector Potential boundaries to set the magnetic vector potential, A_Z, to a constant value on a boundary.

The potential can also be defined as a function of position using math functions. Normally, this type of boundary condition is used to specify the potential of outer boundaries. It can also be used to set the interface between two objects to a potential, modeling the presence of a very thin conductor between the objects. They are sometimes called Dirichlet boundaries.

The behavior of the magnetic field on a Vector Potential boundary depends on whether you define a constant or functional potential on the boundary. Remember that the magnetic vector potential, A, is defined to be a field that satisfies the equation

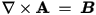
Because the magnetostatic field solver assumes that A has a z-component only and B lies in the xy-plane, the relationship of B to A is given by the following:

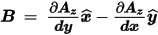
If A_Z is constant along a horizontal boundary, the partial derivatives of A_Z with respect to x will be zero – forcing B to have an x-component only, and be tangential to the boundary. Likewise, if A_Z is constant along a vertical boundary, the partial of A_Z with respect to y will be zero – forcing B to have a y-component only and again indicating that the field will be tangential.

In general, the magnetic field will be tangential to any boundary on which A_Z has been set to a constant.

If the potential is a function of position, the partial derivatives of A_Z with respect to x and y will not necessarily be zero. It all depends on what type of math function was used to specify the potential. Thus, B may not be tangential to the boundary and some flux will cross it.

In eddy current problems, the magnetic vector potential is a time-varying quantity in the form:

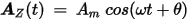
where A_m is the magnitude of the potential and q is its phase angle — its offset from a pure cosine wave. Therefore, when specifying A_Z on a boundary, you must enter both its magnitude and phase. The magnitude and phase of the potential can also be defined as a function of position using math functions.