Screening (Shifted Hammersley Sampling) Optimization
The Screening (Shifted Hammersley Sampling) algorithm is used for sample generation by all methods except NLPQL. The conventional Hammersley sampling algorithm is a quasi-random number generator, which has very low discrepancy and is used for quasi-Monte Carlo simulations.
A low-discrepancy sequence is defined as a sequence of points that approximate the equi-distribution in a multi-dimensional cube in an optimal way. This means that the design space is populated almost uniformly by these sequences and that dimensionality is not a problem because of the inherent properties of Monte Carlo sampling. The number of points does not increase exponentially with an increase in the number of input parameters.
The conventional Hammersley sampling algorithm is constructed by using the radical inverse function. Any integer n can be represented as a sequence of digits n0, n1, n2,..., nm by the following equation:
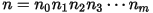
For example, consider the integer 687459, which can be represented this way as n0=6, n1=8, and so on. Because this integer is represented with radix 10, you can write it as 687459=9+5*10+4*100 and so on. In general, for a radix R representation, the equation is:
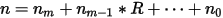
The inverse radical function is defined as the function that generates a fraction in (0, 1) by reversing the order of the digits in the previous equation about the decimal point, as shown.
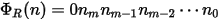
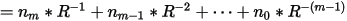
Thus, for a k-dimensional search space, the Hammersley points are given by the following expression:
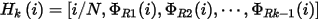
Where i = 0, ..., N indicates the sample points. Now, from the plot of these points, it is seen that the first row (corresponding to the first sample point) of the Hammersley matrix is zero and the last row is not 1. This implies that, for the k-dimensional hypercube, the Hammersley sampler generates a block of points that are skewed more toward the origin of the cube and away from the far edges and faces. To compensate for this bias, a point-shifting process is proposed that shifts all Hammersley points by the amount that follows:
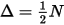
This moves the point set more toward the center of the search space and avoids unnecessary bias. Thus, the initial population always provides unbiased, low-discrepancy coverage of the search space.
