Phasor Notation

Time varying quantities that have the form:

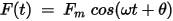
can be represented as rotating phasors in the complex plane. Using Euler’s formula:

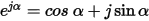
If a = wt+q, F(t) equals the real portion of e^j(wt+q):

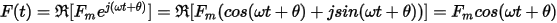
Each time-varying quantity has the form F_me^jqe^jwt. The F_me^jq component is merely a complex constant that can be represented by a stationary phasor in the complex plane. The F_me^jwt component is a complex number that depends on t, and can be represented as a rotating phasor in the complex plane, as shown here.

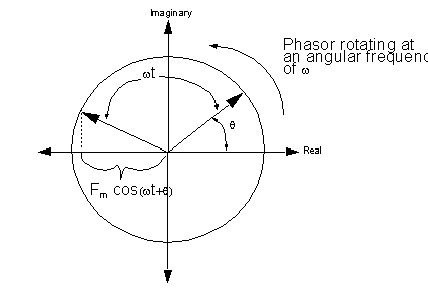
The phasor’s projection on the real axis oscillates sinusoidally. It reaches a peak when parallel with the real axis, and crosses zero when parallel with the imaginary axis. Thus, a phasor with q=90° represents a quantity that peaks 90 degrees after a phasor with q=0°.