Maxwell’s Equations

The eddy current field simulator solves for time harmonic electromagnetic fields governed by Maxwell’s equations:

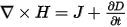
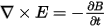
Ñ • D = r

Ñ • B = 0

where:

• E is the electric field.
• D is the electric displacement, eE.
• B is the magnetic flux density.
• H is the magnetic field intensity, B/m.
• J is the conduction current density, sE.
• r is the charge density.

The eddy current solver assumes that all time-varying electromagnetic quantities in the problem have the form:

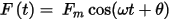
Using Euler’s formula,

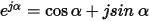
if a = wt+q, F(t) equals the real portion of e^j(wt+q):

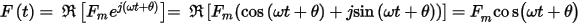
Now, because each time-varying quantity has the form F_me ^jqe ^jwi, ¶D/¶t and ¶B/¶t are equal to jwD and jwB.

Therefore, with this simplification and the relations H = mB, D = eE, and J = sE, Maxwell’s equations reduce to

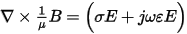
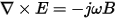
Ñ • eE = r

Ñ • B = 0