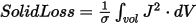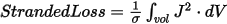Ohmic
loss

Ohmic loss is always associated with conduction current distribution in conductors that are not perfect. Thus, the resistivity of conductors is responsible for the ohmic power loss when current flows in such conductors. It is also called the Joule-Lenz effect. There is always a heating effect due to the ohmic loss, often called Joule heating.

Total loss

Total loss is associated with loss density fields in 2D and 3D magnetic transient solutions only. Total loss uses the total integrated loss output from the solver and averages it, using each solver timestep between the last two consecutive save-field times. It is useful for passing loss density information from Maxwell to the Ansys thermal solvers with fewer save-field times. For Litz Wire only, total loss also includes StrandedLossAC.

Unlike most other loss quantities, which are instantaneous values, total loss is a running average over time, i.e. at time T1 it is calculated with fields from T1 to T2.

Hysteresis
loss

Hysteresis loss is associated with loss density fields in 2D and 3D eddy current solutions only. Hysteresis loss is short for magnetic hysteresis loss and represents power loss in some magnetic materials (electric steels or ferrites) in alternating (sinusoidal) magnetic fields. This loss is due to a phenomenon called "magnetic viscosity" which causes the B and H fields to have a phase shift between them. In the B-H plane, for linear materials, the relationship between these two fields describes an ellipse. The hysteresis loss is proportional to the area of the ellipse.

Dielectric
loss

Dielectric loss is associated with loss density fields in 2D and 3D eddy current solutions only. Dielectric loss or electric hysteresis loss represents power loss in ferroelectric materials (such as barium titanate, lead zirconate titanate) in alternating (sinusoidal) electric fields. This loss is due to a phenomenon called "electric viscosity" which causes the D and E fields to have a phase shift between them. In the D-E plane, for linear materials, the relationship between these two fields describes an ellipse. The dielectric loss is proportional to the area of the ellipse.

SurfaceLoss
Density

The surface loss density is associated with the induced eddy current on the impedance boundary.

Emloss

In 2D and 3D eddy current solvers only: Emloss combines the ohmic loss, dielectric loss, hysteresis loss, and StrandedLossAC (for Litz Wire only).

Edgeloss
density

Edge loss density represents losses associated with impedance boundary applied on conductive surfaces on the boundary of the solution domain or on surface of excluded objects. It assumes an exponential spatial decay (toward the interior of the respective material) of induced current magnitudes and of associated losses. Integrating the loss along the edge produces the entire loss associated with the "edge".

Core
loss

The core loss combines eddy current losses and hysteresis losses for a transient solution type. It is a post-processing calculation, based on already calculated transient magnetic field quantities. It is applicable for the evaluation of core losses in steel laminations (frequently used in applications such as electric machines, transformers) or in power ferrites.

Solid
Loss

The solid loss represents the resistive loss in a 2D or 3D volume and is calculated by

For 2DXY designs, the length is given by Set Model Depth, while for RZ designs the volume is based upon the rotation of the cross-section around the symmetry axis.

Stranded
Loss
(3 types)

There are three types of stranded loss quantities: StrandedLoss, StrandedLossAC, and StrandedLossR, which represent the loss in a 2D or 3D winding utilizing multi-turn coil terminals.

• StrandedLoss is dependent on the object’s material conductivity of a stranded source. It represents the loss due to the DC resistance only and uses the cross-sectional area of the object that is assigned with the excitation. Where J is the current density, it is calculated by

  

  • When Litz wire is not defined, StrandedLoss is computed by assuming fill factor = 100% (the ratio of net conductor area to coil terminal area).
  • When Litz wire is defined, StrandedLoss is computed by using the actual fill factor based on the specified Litz stranding and represents the DC loss only.
  • StrandedLoss does not include the losses of end-coil resistance in 2D.
  • StrandedLoss can be used to scale the loss density to a coupled thermal analysis.

• StrandedLossAC is reported when using Litz wire model, and is dependent on the object’s material conductivity of a stranded source. It represents the loss due to the DC resistance as well as AC eddy current losses due to proximity effects and skin effects.

  • StrandedLossAC = StrandedLoss + AC eddy current losses due to proximity effects and skin effects.
  • StrandedLossAC does not include the losses of end-coil resistance in 2D.
  • StrandedLossAC can be used to transfer loss density to a coupled thermal analysis.
• StrandedLossR represents the loss based on I² times the resistance R, by using the resistance value entered in the Winding properties for a voltage type winding only (Reported for a stranded voltage source not in an external circuit).