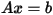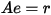Iterative Matrix Solver Technical Details
Two iterative solvers (PCG and QMR) are supported in Maxwell. The PCG is supported in the magnetostatic and electrostatic solvers and QMR is supported in the eddy current solver.
For large simulations, the iterative solvers save significant memory – easily a factor two or more, and may be also faster than the direct solver.
Consider the matrix equation:
|
|
(1) |
where A is a matrix, b is the right-hand side and x is the solution.
When A-1 is computationally expensive or the exact solution x is impossible,
an alternative is to seek an approximation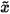 
to x, with an error e = x - 
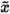. The exact solution can therefore be rewritten
as
|
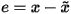
(2) |
Substituting (2) into (1) results in the so-called residual equation:
|
|
(3) |
where r is called the residual defined by
|
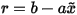
(4) |
As mentioned above, the exact solution for e in (3) is impossible because it requires A-1. However, if an approximation M »͌͌͌͌͌ A is available, the error e can be approximated in (3) by
|
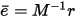
(5) |
Finally, the approximation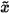 
is updated by
|
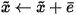
(6) |
It is (4)-(6) that form the foundation of the iterative
solution method. A matrix solver using the iterative solution method
is called an iterative matrix solver.
The method starts with an initial guess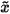 
= x0 and repeats (4)-(6) until the approximation 
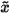to x is within tolerance,
or the number of iterations exceeds a given number. In the former case,
it is said the solution converges; while in the latter, it doesn't.
The residual r is used for measuring the closeness of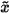 
to x. Because A and b in (1) can be scaled
by the same factor without altering x, so does the residual r in (4). It typically makes more sense
to replace ‖r‖
as the stopping criterion with the relative residual:
|
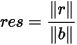
(7) |
where ‖ ‖ stands for vector norm.
M in (5) is called a preconditioner of A. A good preconditioner greatly reduces the number of iterations. The following makes M a good preconditioner: M is a good approximation to A in some sense and M-1 is computationally cheap.
Some of the classic iterative matrix methods include
- The Jacobi method where M is the diagonal of A.
- The Gauss-Seidel method where M is the lower triangular or upper triangular matrix of A.
- The successive over-relaxation method (SOR) where M is a weighted combination of the lower triangular and upper triangular matrix of A.
Refer to the following reference for the details of iterative solvers:
Henk A. van der Vorst, "Iterative Krylov Methods for Large Linear System" Cambridge University Press, 2003.