Irreversible Demagnetization Due to Temperature Change

Permanent magnets exposed to heat can lose strength that cannot be recovered. For example, if a permanent magnet motor is operated under a torque overload condition, the motor will draw more current to produce the required torque. The increased current causes some demagnetization, further increasing the current draw. Over a period of time, this overload may cause the motor to overheat. The resulting rise in temperature can lower the magnet material's intrinsic coercivity, thus making the magnet prone to demagnetization. If the temperature exceeds the magnet's operating point, some of the magnet's domains become permanently demagnetized. Consequently, when the magnet's temperature decreases to its initial value, the operating point does not return to its original value. This effect is irreversible.

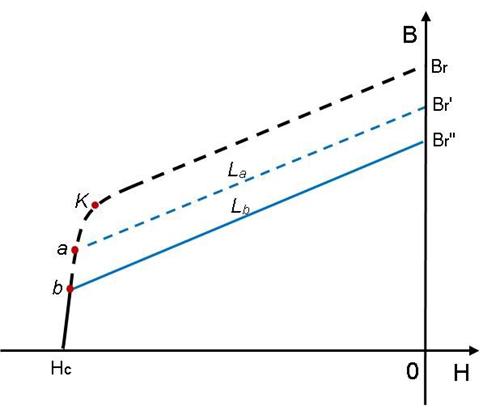
The following image shows that when a new working point a goes below the knee point K, the subsequent working point will change along a new constructed B-H curve, which consists of two curve segments: the recoil line L_a and the demagnetizing curve part below point a. The residual flux density of the recoil line is B_r', and the difference between B_r and B_r' is the irreversible B_r loss, which is denoted as ΔB_r = B_r – B_r'.

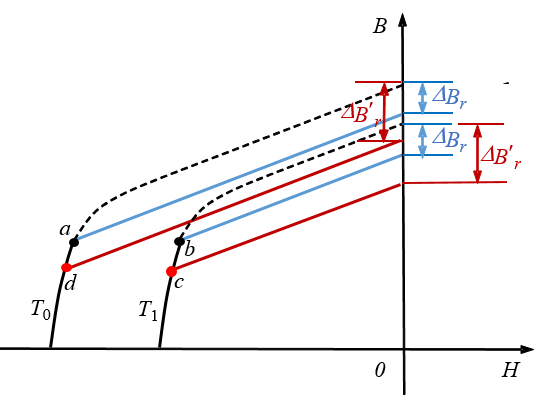
When the temperature of a permanent magnet with operating point a (as shown below) increases from T₀ to T₁, based on user-defined thermal modifiers, a new demagnetization curve can be constructed element by element at the new temperature, T₁. Because the initial irreversible B_r loss ΔBr remains unchanged, the initial operating point on the new demagnetization curve can be identified as point b (the intersection of the new demagnetization curve and the recoil line which passes (B_r – ΔB_r). It follows that the worst-case operating point at temperature T₁ can be further evaluated as indicated by point c from the field solution. This new worst-case operating point, c, causes the irreversible B_r loss to increase from ΔB_r to ΔB'_r. If the temperature then changes from T₁ back to T₀, the operating point will not return to point a. Instead, it will be located at d – associated with temperature T₀ based on the new irreversible loss ΔB'r. The Maxwell solution is able to store the design's irreversible demagnetization values for different working temperatures.