Inductance in Terms of Flux Linkage and Currents

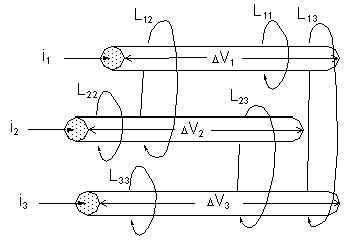
An inductance matrix represents the magnetic flux linkage between the current loops in a system. Given the three current loops below, the relationship between induced flux and currents is as follows:

l₁ = L₁₁ i₁ + L₁₂ i₂ + L₁₃ i₃

l₂ = L₁₂ i₁ + L₂₂ i₂ + L₂₃ i₃

l₃ = L₁₃ i₁ + L₂₃ i₂ + L₃₃ i₃

This can be expressed in matrix form as

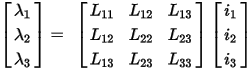
The inductance matrix above gives the relationship between l and i for the three independent current loops. In a device with n current loops, this relationship would be expressed by an n´n inductance matrix. Inductance matrix values are specified in henries.

If one ampere is applied to Current Loop 1 and zero amperes are applied to the other two loops, the inductance matrix becomes

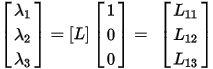
The diagonal terms in the matrix (such as L₁₁) represent the self-inductance of each current loop. Self-inductance is numerically equal to the flux linkage in a current loop when one ampere is flowing in it, and no current is flowing in the other loops. For example, L₁₁ is equal to the flux in Current Loop 1 when one ampere is flowing in that current loop, and no current is flowing in the other loops.

The off-diagonal terms (such as L₁₂, L₁₃) represent the mutual inductances between the current loops. Mutual inductance is numerically equal to the flux linkage in a current loop when one ampere is flowing through another loop, and no current is flowing anywhere else. For example, L₁₂ is equal to the flux linkage in Loop1 when one ampere is applied to Loop 2 and no current is flowing in the other loops.

Note that the inductance matrix is symmetric about the diagonal. This indicates that the mutual effects between any two loops are identical. For instance, L₁₃, the inductance between Current Loop 1 and Current Loop 3, is equal to the inductance between Current Loop 3 and Current Loop 1.