Impedance Matrix
An impedance matrix summarizes the relationship between AC voltages and AC currents in multi-conductor systems. Given the two current loops below, the relationships between voltages and currents in each loop is as follows:
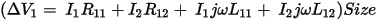
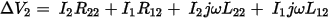
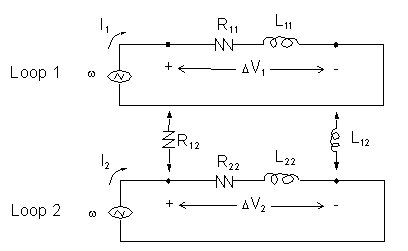
This can be expressed in matrix form as
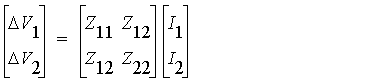
where
- Vi and Ii are phasors.
- Z11 = R11 + jwL11 (the self-impedance of Loop 1).
- Z12 = R12 + jwL12 (the mutual impedance between Loops 1 and 2).
- Z22 = R22 + jwL22 (the self-impedance of Loop 2).
The impedance matrix above gives the relationship between V and I for the two current loops. In a device with n current loops, this relationship would be expressed by an n x n impedance matrix. The matrix values displayed by the software are resistance and inductance (not resistance and reactance) and therefore do not include jw.
where
- w is equal to 2pf, where f is the frequency of the AC current source.
- R is the AC resistance, given in ohms/meter (XY) or ohms (RZ).
- L is the AC inductance, given in henries/meter (XY) or henries (RZ).
Related Topics
Virtual Torques (Eddy Current)
