Harmonic Force Calculation from Maxwell

Maxwell can calculate the harmonic force on each tooth of a rotating machine. This feature enables the one-way coupling between Maxwell and Harmonic Response of Ansys. The force is object based, not element based. The harmonic momentum reference to the geometric center of the object is also provided at the same time. This feature is also extended to any individual object.

There are two options to calculate the force of an individual tooth:

• Split the stator/rotor to form separate tooth object, and integrate forces on all out surfaces of this tooth except the splitting surfaces.
• Draw an arc (2D) or a cylindrical face (3D) near the tooth in the air gap, and integrate forces on this face.

Discrete Fourier Transform (NDFT) with Non-Uniform Time Interval

In the general case, the definition of the Non-uniform Discrete Fourier Transform (NDFT) is the same as the definition with constant time interval, taking into consideration that the samples can be taken at irregular intervals in time (t_n). That is to say that the samples x(k) of the irregular Fourier transform are taken at multiples of a quantity Dw, which is a fixed quantity in the Fourier domain. The fixed quantity, Dw, in the regular case corresponds to 2p/T. The extension from regular to irregular sampling, therefore, depends on the duration of the signal x(t) and not on the fact that the samples are taken at regular or irregular intervals.

A finite sample measured at N points in a period of T:

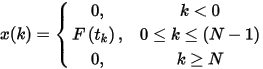
The definition of the non-uniform discrete Fourier transform (NDFT)is as follows:

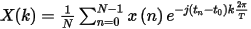
The inverse NDFT is given by

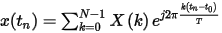
Data Collection

The solver records the components of force and momentum at all teeth at every timestep:

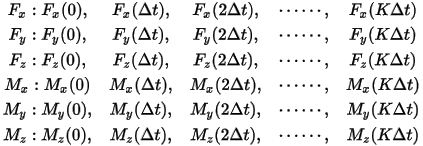
If 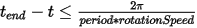, then the solver keeps recording.

Generate Harmonic Force from Partial Model to Full Model

With symmetry-multiplier (period in 3D) > 1, Maxwell solvers automatically generate harmonic force for the full model from the partial model r* = Ar.

where r is the vector to be rotated, r* is the vector after rotation. The rotation matrix in 3D:

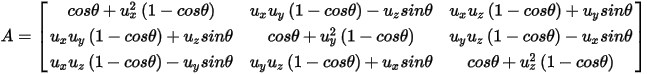
The rotation matrix in 2D:

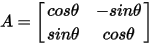
Vectors that need to be rotated: position (r), force (F) and moment (M)

Spatial and Temporal 2D Discrete Fourier Transform (DFT)

Electromagnetic force components on teeth inside an electric machine are spatial (in circumferential direction) and temporal (transient). The magnetic force density acting on the stator along the air gap is dependent on time and on space. This spatial and temporal force distribution can be expanded by means of Fourier analysis to calculate its time and space harmonic waves. This analysis can be used to improve NVH (noise, vibration, and harshness) performance.

The magnetic force density acting on the stator along the air gap is dependent on time and on space. This spatial and temporal force distribution can be expanded by means of Fourier analysis to calculate its time and space harmonic waves.

The force components on teeth can be expressed as function f(x, t), where x represents spatial, and t denotes temporal. The function f (x, t) is decomposed to a linear combination of harmonic (sines and cosines, more generally orthogonal) functions.

Direct Transformation

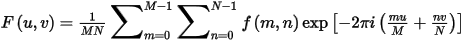
where:

u = 0, 1, …… M-1, wave number in spatial,

v = 0, 1, ……. N-1, wave number in temporal.