Four-Parameter Curve Fitting
The three-parameter curve fitting technique fits the demagnetization curve well. For the nonlinear permanent-magnetic material, the real operating point lies often not on the demagnetization curve, but on the recoil line. The relative recoil magnetic permeability calculated with the three-parameter curve fitting technique will cause deviation, therefore RMxprt employs a more accurate fitting technique: four-parameter curve fitting technique, as introduced below.
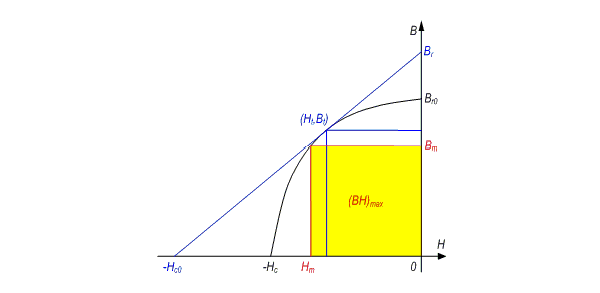
Given the four characteristic parameters Br, Hc, (BH)max and mr, the principles of the four-parameter curve fitting algorithm are summarized as follows:
- Draw a line through the point (0, Br) with the slope equal to -mrmo as shown in the figure. The segment of this line in the second quadrant is termed the ideal recoil line.
- Find the virtual magnetic flux density Br0.
- With Br0, Hc, and (BH)max, draw the demagnetization curve with the three-parameter curve fitting technique. The curve should touch the ideal recoil line at the tangent point (Ht, Bt).
- Any magnetic flux density B in the interval 0 ≤ B ≤ Br corresponds to the magnetic field intensity H:
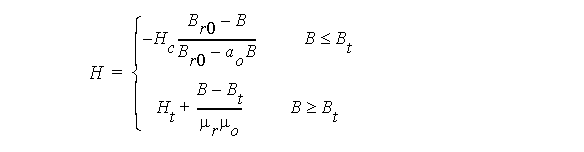
The virtual magnetic flux density Br0 is found by iteration:
- Start from the initial guess for the
lower and the upper bounds for the virtual magnetic flux density Br0:
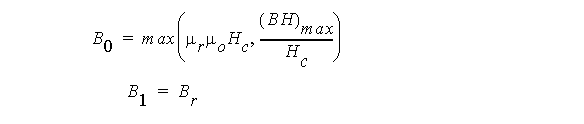
- Let
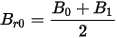
- With Br0, Hc, and (BH)max, draw the demagnetization
curve with the three-parameter curve fitting technique.
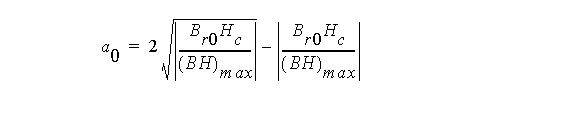
- The curve should touch a line
parallel to the ideal recoil line at the tangent point (Ht, Bt).
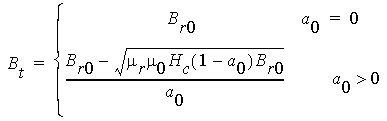
and
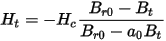
For any magnetic flux density B in the interval 0 ≤ B ≤ Br, the corresponding magnetic field intensity H will be calculated by:
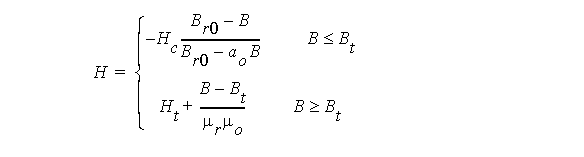
- Calculate the value of Hr corresponding to Br using:
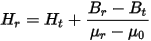
- If Hr > 0, the assumed virtual Br0 is too small, the lower bound of the interval needs to be increased, so let B0 = Br0. If, however, Hr < 0, the assumed Br0 is too big, the upper bound of the interval needs to be decreased, so let B1 = Br0.
- Repeat steps (2) through (7) until Hr converges to 0 within satisfactory precision.
