Force Densities in Maxwell

Let T_αβ be the Maxwell stress tensor (refer to reference [1] for detail of the Maxwell stress tensor). Then the force acting on an object can be calculated by

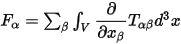
(1)

Application of the divergence theorem to volume integral gives

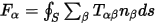
(2)

Note that 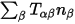is the force per unit area transmitted across the surface. Namely, it is the surface force density, which is denoted as

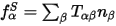
(3)

Also, from (1), you can define a volume force density by stress tensor as

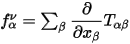
(4)

For a magnetostatic field (similar forms for electric field), the explicit form of the Maxwell stress tensor is

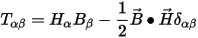
(5)

So the surface force density can be calculated as

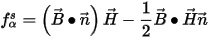
(6)

The volume force density can be calculated by (4) and using the virtual work principle (refer to reference [2] for details).

Reference [1] J.D. Jackson, Classical Electrodynamics, 3rd edition, Wiley, 1999.

Reference [2] A. Bossavit: "Eddy-currents and forces in deformable conductors", in Mechanical Modelings of New Electromagnetic Materials (Proc. IUTAM Symp., Stockholm, April 1990, R.K.T. Hsieh, ed.), Elsevier (Amsterdam), 1990, pp. 235-42.