Electric Field Calculation

The Electric field solver uses the electric scalar potential values as DOFs. There are two basic types of static electric field solutions, as well as the combination of these two:

For the electrostatic solution, it is assumed that all objects are stationary (velocity is zero everywhere in the space where the electrostatic field is calculated), there is no time variation of any of the electromagnetic quantities (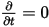) and there is no current flow in conductors (conductors are in electrostatic equilibrium) and thus Joule losses are zero everywhere. All conductors are considered to be perfect and equipotential such that there is no electric field inside conductors. The unknowns (DOFs) are electric scalar potentials at all the nodes of the tetrahedra of the mesh. The distribution of conductivity in the space of the problem is irrelevant, only the distribution of permittivity is relevant for the solution process.

Note: For the electrostatic solution, if two or more conductors touch each other, they should be united into one object by using the Modeler Boolean operation "Unite" before analysis.

For the DC current flow solution, only the conductors (with electric conductivity s > Insulator/Conductor Threshold) are considered in the solution process. The DOFs are also the electric scalar potentials at the nodes of the mesh. Here the distribution of electric conductivity is relevant for the solution process while the permittivity is irrelevant. There is DC current flow in conductors (conductors are not equipotential) and there is non-zero Joule loss (ohmic power loss) in the conductors (which are part of an excited current path). The conductors are considered to be immobile (velocity is zero everywhere). The magnetic field associated with the DC current flow is not calculated and is totally decoupled from the calculated electric field distribution in conductors.
The combination of the DC current flow and electrostatic solution is based on the division of the arrangement into conductors and insulators. Conductors are those objects whose electric conductivity s is greater then or equal to the Insulator/Conductor threshold, and insulators are those whose conductivity s is less then the Insulator/Conductor threshold. The solution of such problems is performed in two steps: first the DC conduction problem in the conductors is computed, then the electrostatic solution in insulators is calculated using the electric scalar potential of the conductors as a voltage boundary condition.

For the electric field solution, there are ten nodal DOFs (electric scalar potential unknowns) associated with each tetrahedron at each of the four vertices and at each of the six mid-edge nodes. Therefore, a quadratic approximation of the electric scalar potential inside each tetrahedron can be obtained.

The electrostatic field solver solves a Poisson type partial differential equation for the electric potential unknown, F, with appropriate boundary conditions:

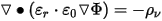
where

F(x,y,x) is the electric potential scalar function of position.
e_r(x,y,x) is the relative permittivity, which is a function of position and can be isotropic or orthotropic. (e₀= 8.854x10^-12)
F/m is the permittivity of a vacuum.
r_n(x,y,x) is the volume density of the electric charge.

Once the electric potential is obtained by solving the above second order differential equation in the domain of the problem, Maxwell's equations and the applicable constitutive equation are then used to obtain the electric field strength, 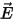, and electric flux density, 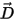, vectors, as follows:

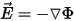
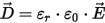
Typical sources for electrostatic problems are net charges (assumed to have a uniform distribution) applied to perfect insulator model objects or on surfaces that cannot touch conductors and voltages (electric potential applied to perfect conductor model objects or on surfaces, also called a Dirichlet boundary condition). Additionally, a floating boundary condition can be applied to perfect conductors (surrounded by insulators) or to surfaces surrounded by perfect insulators.

Volume charge density is another allowed excitation, which can have a spatial distribution specified by the user and can be applied to insulating objects only that do not touch conductors.

At the interface between two dielectrics, the normal component of the electric flux density vector has no jump if the charge density at the respective interface is zero:

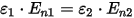
where the permittivity and normal electric field values are considered in the two dielectrics and are designated by the subscripts 1 and 2. Alternatively, when crossing a surface with non-zero charge density, the normal component of the electric flux density has a jump equal to the respective local superficial charge density. It follows that in dielectrics (such as air, for example) in the immediate vicinity of conductive objects (perfect conductors), the (normal) component of the electric flux density is equal to the neighboring local charge density on the metallic surface (since in metallic objects the field value is zero).

Note: When voltages are applied to conductors, the charge transferred from the DC source(s) to the conductors almost instantly receives a superficial distribution. For real (good) conductors, the time constant for the diffusion of the charge is of the order of 10^-19 s. Therefore, for all practical instances, the charge relaxation process is considered to occur instantly. Once the charge on conductors reaches the steady state (almost instantaneously), the electric field in the neighboring dielectrics has a distribution that is governed by the laws of electrostatics, and the field in conductors is null while the field distribution in dielectrics is dictated – as far as material properties are concerned – by the respective permittivities and is independent of the conductivity of the electric conductors. This is why, in electrostatics, real conductors can be considered as perfect conductors.

Electrostatic regime of the electromagnetic field is rarely achieved in practice rigorously speaking. However, very good approximations can be used for practical situations within the limits specified above.

The DC current flow solver solves the equation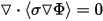

where

F(x,y,x) is the electric potential scalar function of position.
s(x,y,z) is the electric conductivity (in SI it is measured in S/m), which is a function of position and can be isotropic or orthotropic.

Once the electric potential is obtained by solving the above second order differential equation in the domain of the problem, Maxwell's equations and the applicable constitutive equation (Ohm's law in a local formulation) are then used to obtain the electric field strength and the electric current density 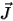vectors:

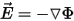
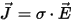
Typical sources for DC current flow problems are currents applied on surfaces of conductors and voltages (electric potential applied to surfaces of conductors). The direction of the applied current is either "in" or "out", always normal to the respective surfaces.

Note: Multiple conduction paths are allowed. Each conduction path that has a current excitation must also have either a voltage applied or a sink to ensure a unique solution.

The sink is a particular excitation (without a numerical value assigned to it) that is used to ensure the divergence-free character of the calculated DC current density vector in each conduction path.

At the interface between two different conductors, the normal component of the current density vector is continuous: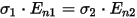

For DC current flow problems, the solution is dictated everywhere inside the conductors by the distribution of electric conductivity, as far as material properties are concerned.

Charge, voltage, floating, current, and sink type excitations are called "terminal" type excitations since they can be referenced in a matrix extraction setup.

In perfect conductors, no computation occurs, and the electric scalar potential (the unknown in the problem) has a uniform value. However, in the post-processing phase, the (constant) distribution of the electric scalar potential (voltage) is correctly rendered. No solution is available in solids explicitly excluded from the solution.

The solution of any field problem is only possible if appropriate boundary conditions have been set. The boundary conditions have three purposes:

Boundary conditions are always necessary from a mathematical perspective in order to ensure the uniqueness of the solution calculated by Maxwell.
Boundary conditions occasionally represent a convenient way of modeling different ideal situations. For example, in order to model the field in a dielectric sandwiched between two very thin conducting objects (the thickness is at least two orders of magnitude less than the other relevant dimensions of the respective conducting objects), only the two respective surfaces need to be modeled on either side of the dielectric object. In the setup, those top and bottom surfaces carry appropriate boundary conditions, and the field in the dielectric is correctly simulated without having to draw the respective conductors.
Boundary conditions also occasionally provide a convenient way of taking advantage of symmetry situations. In such cases, the models must have the same geometric and material properties, as well as electric symmetry.

Typical boundary conditions include voltage, floating, and insulation boundary conditions. In the case of an insulating boundary condition, a conductor must exist at least on one of the sides of the respective surface.

The default boundary condition applied to all faces of the boundary of the electric field (static or stationary) problem is a Neumann homogeneous condition. This condition enforces an electric field tangent behavior of the solution in the immediate vicinity of the boundaries. 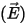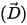There is no need to apply any particular boundary condition at the interface between objects with different material properties, as the solution automatically ensures – in average – the continuity of the tangential component of the electric field strength and the continuity of the normal component of the electric flux density vector across surfaces with zero superficial electric charge density (for electrostatic problems).