Axisymmetric Field Simulation

If you selected Cylindrical About Z as the geometry mode when setting the solution type, a special version of the selected field solver is used. It assumes that the 2D geometry being studied sweeps 360° around the z-axis of a cylindrical coordinate system, enabling you to model devices like solenoids and insulators that have an axis of rotational symmetry. All electric or magnetic fields in the problem must also be rotationally symmetric so that the solution in any RZ-plane is the same as any other.

Note: All cylindrical about Z models must be drawn in the XZ plane with X ≥ 0.

Axisymmetric field simulation is available for the following solvers:

Electrostatic
Magnetostatic
Eddy Current
DC Conduction
AC Conduction
Transient with and without motion

Any field solution involving a long plank-shaped object is different from a solution involving an annular object — even though the same equation is solved for both types of geometries. Mathematically, the difference between Cartesian and axisymmetric field solutions arises from the difference in how gradients, curls and divergences are expressed in the two coordinate systems.

In a Cartesian (xyz) coordinate system, these operators are defined as follows (where F is a scalar quantity and F is a vector quantity):

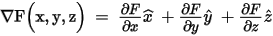
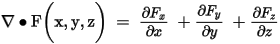
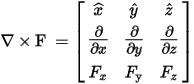
If F has a z-component only, the curl is defined as

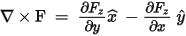
In a cylindrical (r, F, z) coordinate system, these operators are defined as

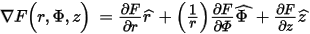
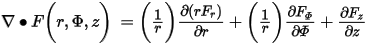
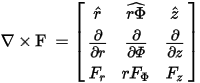
If F has a F-component only, the curl is defined as

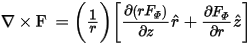
In the cylindrical case, an extra r shows up in places where there is no analogous x in the Cartesian case, resulting in a different field solution. The calculations involving the differences in mathematics between axisymmetric and Cartesian models are implicitly handled by the Maxwell and are transparent to you.