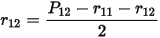AC Loss Effects of Litz Wire on Impedance Matrix
The impedance matrix of polyphase windings is expressed as
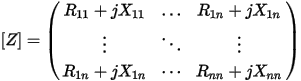
where n is the number of windings.
Litz wire eddy current losses are computed in during postprocessing. When the total number of windings includes some Litz wire windings, the final AC impedance matrix, including an additional resistance matrix due to Litz wire eddy current losses, is expressed as
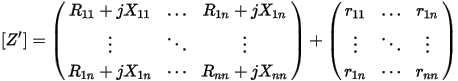
where resistances denoted by rij are additional Litz wire eddy current resistance components.
To compute Litz wire eddy current resistance components, a permeability freezing algorithm is needed. After nonlinear iteration is convergent and permeabilities in all mesh components are frozen, the original impedance matrix [Z] is derived by injecting 1 A exciting current into each phase winding one by one. The self-impedance is obtained from the induced voltage in the excited winding, and all mutual impedances are obtained from the induced voltages in all other windings.
However, the Litz wire eddy current resistance matrix is derived in a different way. When a winding is excited with 1 A rms current and all other windings with zero-value currents, the value of the total eddy current loss (no matter in the excited winding, or in other zero current windings), is the value of the self-resistance. That is, if I1 = 1 A rms current in winding 1 produces total eddy current loss P1, then the self-resistance of winding 1 is
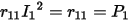
Similarly, if I2 = 1 A rms current in winding 2 produces total eddy-current loss P2, then the self-resistance of winding 2 is
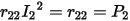
To calculate the mutual resistance between winding 1 and winding 2, 1 A currents in both winding 1 and winding 2 need to be injected. In such a case, the total eddy-current loss is
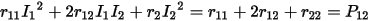
where P12 is the total eddy current loss in all Litz wire windings caused by 1 A currents in both winding 1 and winding 2. Therefore,