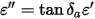3D AC Conduction Solver

AC conduction analysis is the study of

• electric field,
• losses arising in conductors and imperfect (lossy) dielectrics from the application of an alternating (AC) voltage or external current to the electrodes, and

• C and G parameters extraction.

In this harmonic formulation, the magnetic fields are considered negligible, and the electromagnetic field can be treated as electroquasistatic. The electric field is derived from the electric scalar potential F.

One can use this analysis to determine the voltage, electric field, electric flux density, and electric current density distributions, capacitive effects, extract the C and G parameters in electric devices as a function of frequency in response to time-harmonic loading.

Complex equations are used to represent harmonic time-dependency as outlined below.

Governing Equations

Given the Ampere’s Law in frequency domain,

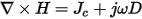
it is possible to obtain the continuity equation solved by the 3D AC conduction solver,

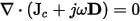
where

• H is the magnetic field
• J_c is the conduction current density
• w is the angular frequency at which the potential is oscillating
• D is the displacement flux density.

Constitutive Relations

The constitutive relations are given by

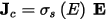
and

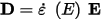
where:

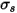• is the static field electrical conductivity
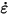• is the complex dielectric permittivity: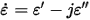

Continuity equation including lossy domains

Applying the above constitutive relations in the continuity equation, one obtains:

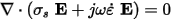
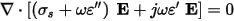
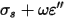represents the equivalent conductivity (s_e) composed by a static (s_s) and an alternating (s_a) part, which is caused by dipole rotation when the material is submitted to an alternating electrical field.

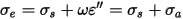
Finally, the continuity equation can be written as:

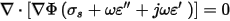
It is of importance to mention that normally the dielectric lossy materials are defined in terms of the dielectric loss tangent (tan d). In this case, the alternating tan d is considered:

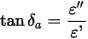
Consequently,