Iterative Matrix Solver Technical Details

The iterative solver always saves significant memory - easily a factor two with simulations of intermediate size, and more with larger simulations. It is also faster than the multi-frontal solver with large simulations.

The following table shows asymptotic behavior with large simulations. N = number of unknowns. This shows that the iterative solver has a better asymptotic behavior both in RAM and in time.

The iterative solver uses a preconditioner that is based on the next-lower order. Therefore, there is no iterative solver option when you solve with zeroth order.

Consider the matrix equation

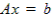
(1)

where A is a matrix, b a right hand side and x the solution.

When A^-1is computationally expensive or the exact solution x is impossible, an alternative is to seek an approximation 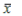to x, with an error 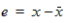. The exact solution can therefore be rewritten as

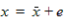
(2)

Substituting (2) into (1) results in the so called residual equation

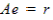
(3)

where r is the residual defined by

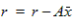
(4)

As aforementioned, the exact solution for e in (3) is impossible since it requires A^-1. However, if an approximation 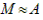is available, the error e can be approximated in (3) by

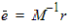
(5)

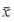
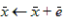
(6)

It is (4)-(6) that form the foundation of the iterative solution method. A matrix solver using the iterative solution method is called an iterative matrix solver. The method starts with an initial guess 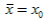and repeats (4)-(6) until the approximation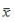to x is within tolerance, or the number of iterations exceeds a given number. In the former case, it is said the solution converges; while in the latter, it doesn't.

The residual r is used for measuring the closeness of 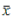to x. Since A and b in (1) can be scaled by the same factor without altering x, so does the residual r in (4). It typically makes more sense to replace ||r|| as the stopping criterion with the relative residual:

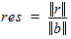
(7)

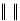
M in (5) is called a preconditioner of A. A good preconditioner greatly reduces the number of iterations. The following makes M a good preconditioner: M is very similar to A in eigen spectrum and 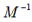is computationally cheap. Some of the classic iterative matrix methods include: the Jacobi method where M is the diagonal of A, the Gauss-Seidel method where M is the lower triangular or upper triangular matrix of A and the successive over-relaxation method (SOR) where M is a weighted combination of the lower triangular and upper triangular matrix of A.

In the iterative method, the major storage is for matrix A and for preconditioner M. The major operation is a matrix-vector multiplication in (4). The computational cost is S+mnT, where S is the number of operations for setting up the preconditioner,m the number of right hand sides, n the average number of iterations per right hand side and T the number of operations for each iteration.

Details of the iterative solver in HFSS are given in:

D. K. Sun, J. F. Lee and Z. J. Cendes, "Construction of nearly orthogonal Nedelec bases for rapid convergence with multilevel preconditioned solvers", SIAM Journal on Scientific Computing, Vol. 23, No. 4, pp. 1053-1076, 2001.

I. Bardi, G. Peng and Z.J. Cendes, "Improvements in Adaptive Mesh Refinement and Multi-level methods in High Frequency Electromagnetics", ACES Symposium, 2002.