Djordjevic-Sarkar Causal Dielectric Model

From the paper "Wideband Frequency-Domain Characterization of FR-4 and Time-Domain Causality" (A. R. Djordjevic, R. D. Biljic, V. D. Likar-Smiljani, and T. K. Sarkar, IEEE Trans. on Electromagnetic Compatibility, Nov. 2001, p. 662), the following simple analytic model was proposed for the frequency dependence of the complex relative permittivity in FR-4 dielectric materials:

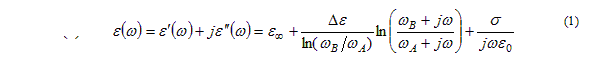
where

This model is an analytic function and, hence, causal in the time domain. It is very simple and only five parameters define it.

The loss tangent is defined as follows:

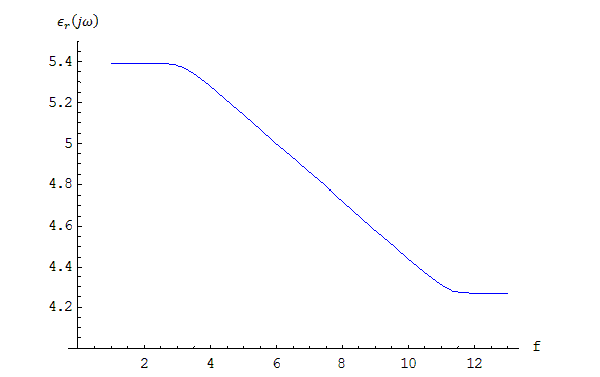
The behavior of the real part of permittivity versus frequency using the Djordjevic-Sarkar model is given by way of the following plot:

The loss tangent predicted by the model (for the case s = 0) is shown in the following diagram.

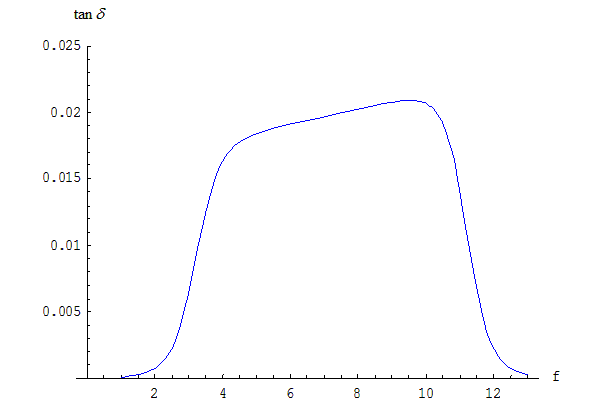
Notice that both curves have two transition frequencies, the first around 10³ Hz and the second around 10¹¹ Hz.

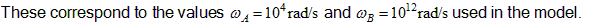
The lower transition frequency is evident in the experimental data for FR-4; the upper transition frequency is best thought of as a fitting parameter. Measured data for FR-4 up to 10 GHz does not show the upper transition frequency. Typically, the upper transition frequency is placed at very high frequency, beyond the limits of practical interest.

Another major feature of the model is the loss tangent is approximately constant between the two transition frequencies. This constant loss tangent behavior is also observed experimentally in FR-4, except at low frequencies where it decreases. At very low frequency the loss tangent starts to rise again due to nonzero DC conductivity.

Djordjevic-Sarkar Model Parameter Calculation

The model parameters can be calculated if the following information about the material is known:

DC conductivity, s_DC (optional; default value is 0)
DC permittivity, e_DC (optional; you have to select the default.)
A triplet of real numbers, consisting of
The measurement frequency w₁
The real permittivity e₁ at this frequency
The loss tangent tan d₁ at this frequency

Knowing the imaginary part of e(w₁) = -e₁. tand₁. Therefore getting,

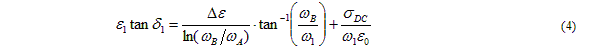
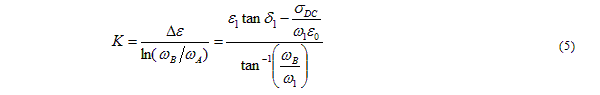
The following equation for the real part also holds:

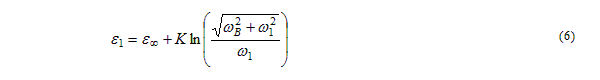
Inserting this expression allows us to solve for the high-frequency permittivity:

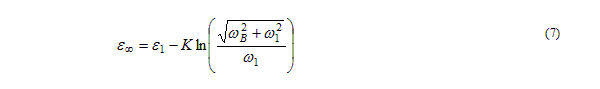
Check the computed value of lower transition frequency to ensure that it is much less than the measurement frequency. If not, raise the DC permittivity; this reduces the value of the lower transition frequency. If you do not know the DC permittivity value, you may select one yourself to satisfy the condition:

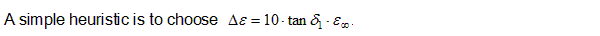
Expressions for Permittivity and Conductivity

The final expressions are as follows:

Relative Permittivity:

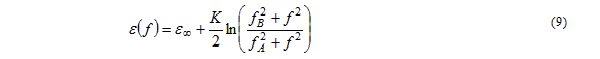
Conductivity:

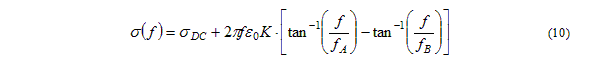
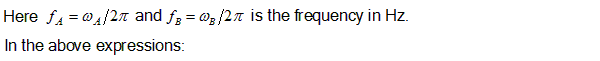
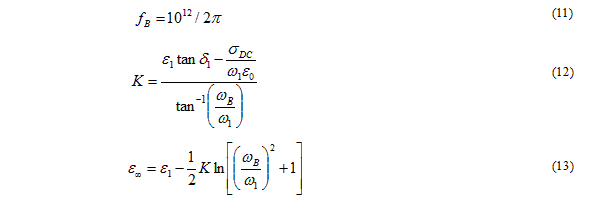
Check the Limit for Input Parameters

The slope parameter K must be > 0. Therefore you must have

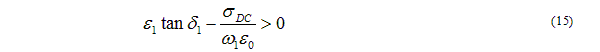
This can occur if you enter a DC conductivity higher than the effective conductivity at the measurement frequency. This is impossible in the Djordjevic model, because its conductivity increases monotonically with frequency. Another way for it to happen is for the measurement frequency to be too low (e.g., Hz instead of GHz) or for the permittivity value to be unreasonably low.

Therefore from (5) and (7) the following is true.

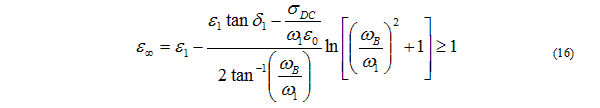
Define the quantity

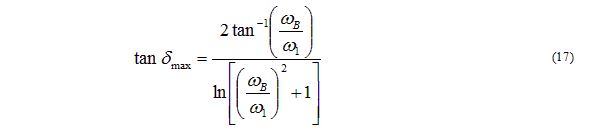
Using this in 16 simplifies the expression as follows.

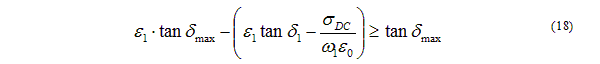
Then, the condition for passivity can be written as follows:

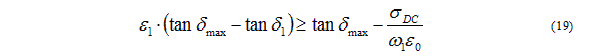
For this to hold, with e > 0, the following two conditions are appropriate

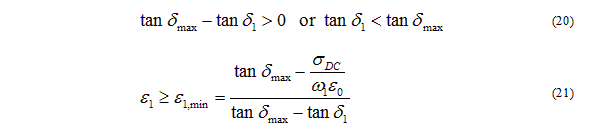
You see on the expression for tan d_max given in (17) the maximum loss tangent is a function of only the upper corner frequency and the measurement frequency.

Reducing the upper corner frequency increases the value of tan d_max at least as long as the following condition is realized.

But reducing the upper corner frequency is not very attractive, because it has not been observed in experimental data. Therefore it is an upper bound on the loss tangents the Djordjevic-Sarkar model can handle. Equation (21) indicates that if the permittivity is too low, the optical permittivity goes below 1. If this condition is violated, two possible fixes are to raise the value of e or to reduce the measurement frequency. But by the same argument as before, reducing the upper corner frequency is not attractive and it is the minimum value of the permittivity. If you reduce the value of the measured loss tangent; this makes the denominator in (21) larger and lowers the value of e_1,_min.

For more information, see Djordjevic-Sarkar Model Parameter Calculation.