VerifEye Technical Notes

VerifEye analysis is a statistical eye-analysis algorithm, similar to the public domain Stat Eye (See QuickEye and VerifEye References for a citation). VerifEye calculates the bit error rate from an analysis of the probability density function for the receiver voltage. VerifEye incorporates the effects of intersymbol interference (ISI) by considering how transitions that preceded the current bit could affect the receiver voltage, given the step response.

For example, suppose the current receiver bit is a 1. This can happen in two ways: either the previous bit was a 1, in which case there was no transition, or the previous bit was a 0, in which case there was a low-to-high transition. In the first case, the receiver voltage is very near to V_HI, the voltage representing a “1” bit. In the second case, the voltage does not reach V_HI due to the slow rise time of the step response at the end of the channel. If the bits are independent, the probability of a transition here is 0.5. Statistically, therefore, the waveform has a 50% chance of having no deviation, and a 50% chance of having a negative deviation.

Chain this process forward and backward, considering each possible transition in turn. However, even if the bits are independent, the transitions are not. A high-to-low transition must be followed by a low-to-high transition and vice versa. VerifEye calculates conditional probabilities including all the possible cases.

The results are probability distribution functions (PDFs) for the voltage value of the rising and falling waveforms. The probability density function p_V(v) gives the probability of obtaining a particular voltage at the receiver at some sample time tau (t). Figure 1 shows an artificial example.

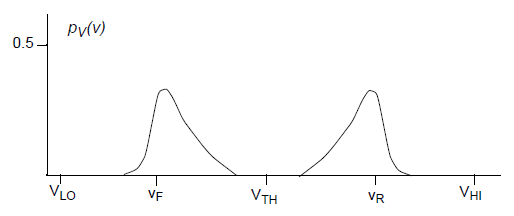
Figure 1. Probability Density Function for Receiver Voltage at Sample Time t

The distribution of p_V(v) is bimodal. The lobe on the left is the PDF for the falling waveform at the given sample time. The lobe on the right is the PDF for the rising waveform at the sample time.

If the channel are purely lossless, the two lobes is narrow peaks. The preceding figure,shows some spreading of the distributions due to intersymbol interference (ISI), jitter, and other factors that causes the voltage to vary around the ideal values. The effect of ISI is to spread the distribution toward the threshold voltage.

Represent the receiver voltage PDF with formulas. Let B_TX be the logic value (0 or 1) of the transmitted bit, and let B_RX be the logic value (0 or 1) of the received bit. The left lobe Figure 1 is the PDF of the receiver voltage when the transmitted bit was a 0, or in probability notation:

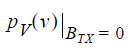
The right lobe is the receiver voltage PDF when the transmitted bit was a 1, or:

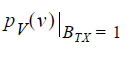
Since B_TX must be either 0 or 1, the total area under the PDF is unity:

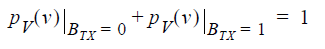
If the bit values are independent, the two lobes are equal in area.

The bit error rate (BER) depends on the threshold voltage. Let V_TH be the threshold voltage that determines whether the receiver bit B_RX is a 1 or a 0. The bit error rate at sample time t is the area under the PDF that is above V_TH when the transmitted bit B_TX is a 0, plus the area of the PDF that is under V_TH when B_TX is a 1, all divided by the total area under both lobes. Since the total area under the PDF is unity, the area of the overlapping regions equals the bit error rate.

Consider just the left lobe of the PDF, the voltage lobe when the transmitted bit is a zero. Figure 2 shows a PDF for B_TX=0, with a tail that overlaps the threshold (the area of overlap is exaggerated for effect).

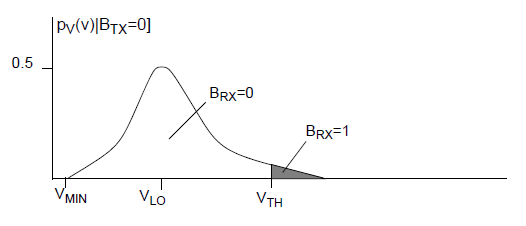
Figure 2. PDF with Bit Error Rate.

The area under the curve that lies under the threshold V_TH is the probability that the received bit is correctly received as a 0. The shaded region in Figure 2 represents the probability that the received bit is incorrectly read as a 1 when the transmitted bit is a 0.

The area of the shaded region represents the probability:

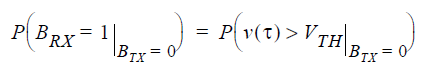
Where P() signifies a simple probability rather than a density function.

If the PDF lobe for B_TX=1 also has a tail that falls under the threshold, the area of the error region represents the following probability:

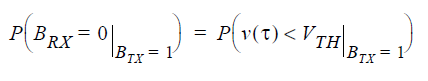
The sum of the two probabilities is the bit error rate at the specified threshold voltage V_TH and at the specified sample time t.

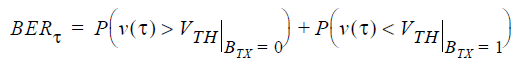
When BER_t is plotted over all values of sample time t from 0 to 1UI, the result is the familiar bathtub curve (Figure 3). Each point on the curve shows the probability that the received bit B_RX fails to equal the transmitted bit B_TX for some value of the threshold voltage V_TH, at sample time t. In Figure 3, the Y-axis uses logarithmic scaling.

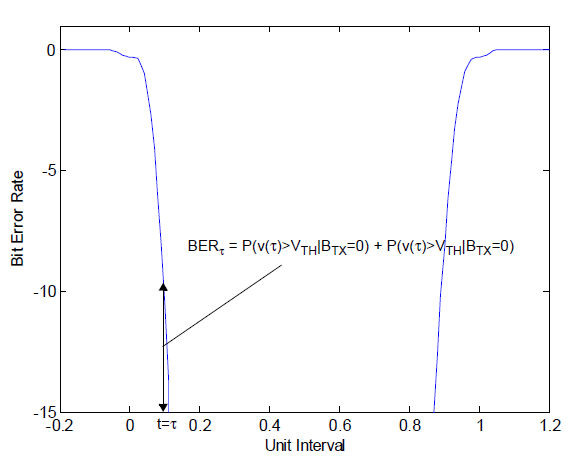
Figure 3. A Bathtub Curve of Bit Error Rate (BER) at Threshold Voltage V _TH.

The integral of the BER curve over threshold voltages (V_MIN < V_TH < V_MAX) produces the cumulative distribution function (CDF) of the receiver voltage. A plot of the CDF is the 3D bathtub or contour plot.