The Bit Error Rate

The bit error rate (BER) is the figure of merit for signal integrity issues. The transmitter sends a sequence of bits through a channel to the receiver. In a perfect channel, every received bit value (0 or 1) is equal to the transmitted value. In the typical channel, some bit errors occur. The BER is the ratio of bits incorrectly received to the total number of bits transmitted.

Inter-symbol interference (ISI) is the major cause of bit errors. ISI occurs when the response of the channel to a change in bit value (from 0 to 1 or from 1 to 0) is longer than the unit interval (UI) or bit time. When a transition takes more than one UI to settle, the values of previous bits affect the waveform for the current bit.

Here is a simple example. Suppose the channel to analyze is a 100-ohm differential driver feeding into an R-C load with R=100 ohms and C=40 pF. Figure 1 shows the input bit sequence to the channel. 1V represents a logic “1”, while -1V represents a logic “0”. The unit interval (UI) is 1ns.

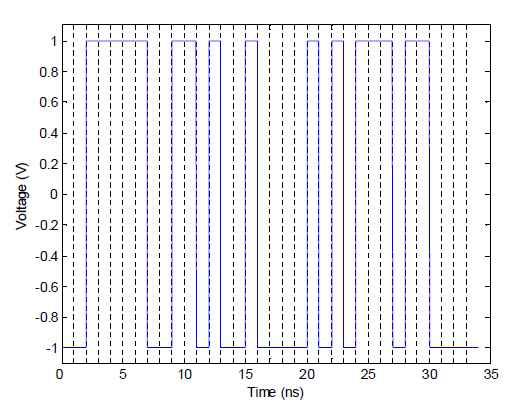
Figure 1: Input to Simple R-C Channel.

Figure 2 graphs the measured output at the receiver end of the channel, showing the degradation of the original stream of bits as it goes through the channel.

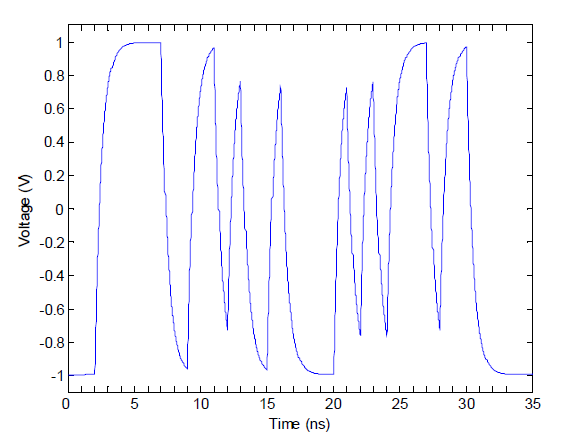
Figure 2: The output of the simple R-C channel.

The waveform in Figure 2 shows the effects of intersymbol interference (ISI). With this channel, the waveform for an isolated 1 surrounded by zeros never gets close to the nominal +1V value, and an isolated 0 surrounded by ones does not fall to -1V. Clearly, this channel has a non-zero bit error rate.

The eye diagram is a convenient tool for estimating the BER given the waveform. Copies of the waveform generated at the receiver end of the channel are overlaid at a spacing of one unit interval (UI). The eye diagram illustrates the allowable window for distinguishing bits from each other at the receiver end. The width and height of the eye opening are the dimensions of the window. The minimum allowable width of the eye depends on the jitter budget. The required height of the window is given by the noise margin of the receivers. Given the required width and height, how often does the waveform violate this window? This is the Bit-Error Rate, or BER.

Figure 3 shows the eye diagram created by shifting and overlaying the waveform of Figure 2.
The area of white space in the center is the eye. (More bits is needed to obtain a better “eye.”)

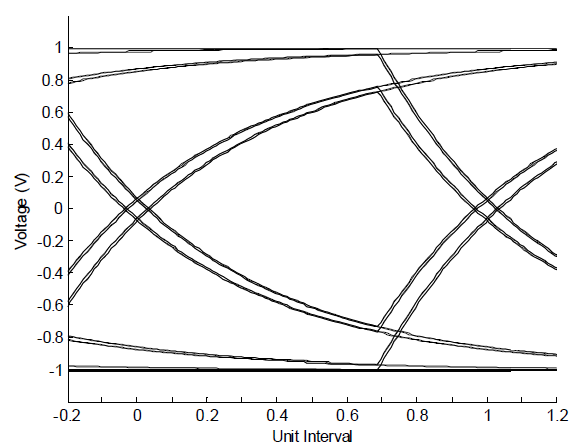
Figure 3: Eye Diagram for Simple R-C Channel

Traditionally, eye diagrams have been measured in the lab or simulated with transient analysis. However, with increasing data rates, particularly in the case of high-speed serial links, the required BER has decreased significantly. The need to predict very low BERs leads to a corresponding increase in the number of bits to be simulated, and thus to a search for alternatives.

The probability that a waveform violates the eye window can be measured from test data or calculated from channel parameters. Both transient analysis and QuickEye measure the BER probability by running sufficient data and counting errors. Quick Eye analysis uses simplifying assumptions to speed up the simulation, but requires the same large data sets to measure low BERs. VerifEye analysis uses a fully statistical approach to calculate the BER without requiring any test data.