QuickEye Technical Notes

Quick Eye analysis employs pattern-dependent convolution. The step responses are simulated with transient analysis for a single rising edge and a single falling edge. The step responses are then combined with the data stream to create an intermediate waveform that approximates the behavior of the fully simulated channel. With QuickEye, inter-symbol interference (ISI) is easy to calculate, but random transmit jitter is more difficult to handle.

QuickEye convolves the step responses for rising and falling edges with the time derivative of the input waveform to calculate the output. Here is a brief derivation.

The output of the LTI channel on the input and the impulse response once more:

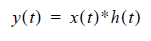
From the assumption of superposition, the impulse response h(t) is the time derivative of the step response u(t). This allows the following substitution:

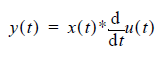
We can transform this formula into the complex frequency s domain by applying the Laplace transform to both sides:

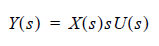
Where Y(s) and X(s) are the Laplace transforms of y(t) and x(t), and sU(s) is the Laplace transform of du(t)/dt. Rearranging the product terms, to get:

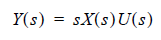
Take the inverse Laplace transform of both sides to obtain the formula used by QuickEye:

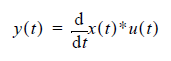
This formulation captures the edge-based nature of the calculation, since the derivative dx(t)/dt is non-zero only during the transitions.

QuickEye creates an intermediate waveform by applying the rising and falling step responses to the transitions in the input data. Figure 1 shows the intermediate QuickEye waveform for the RC example. Rising edges are solid, falling edges are dashed. Summing these transitions creates the waveform in Figure 2.

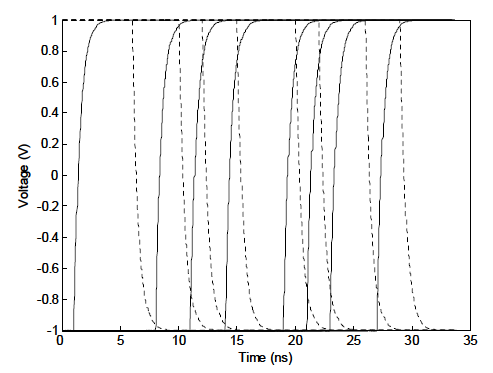
Figure 1. QE Intermediate Waveform for RC Example Data

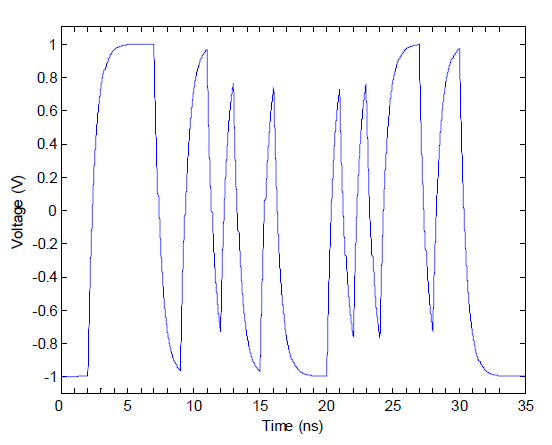
Figure 2: The RC Waveform as Simulated with Transient Analysis

QuickEye overlays the unit intervals on the intermediate waveform to generate the eye diagram. The input bit pattern can be a literal bit list specified in the netlist, a sequence of random bits, a bit pattern read from a file, a pseudo-random selection of bit patterns, or the worst-case bit pattern calculated by peak distortion analysis. (See Eye Source Bit Data and Peak Distortion Analysis).

QuickEye calculates the bit error rate by comparing the data received to the data sent, and counting the number of errors. For a given set of data, the QuickEye convolution algorithm is faster than full transient analysis. Like transient analysis, however, QuickEye requires gigabit run sizes to determine BER values in the 10^-12 range. This practical limitation is the reason for VerifEye.