Plotting Circuit Spectral Domain Data

After transient analysis, one can exam frequency components of the signal of interest by plotting spectral domain data on the Reporter.

1. Open a project in Project Manager window.
2. Right-click Results.
3. In Solution, choose NexximTransient.
4. In Domain, choose Spectral. Several fields appear in the Report window:

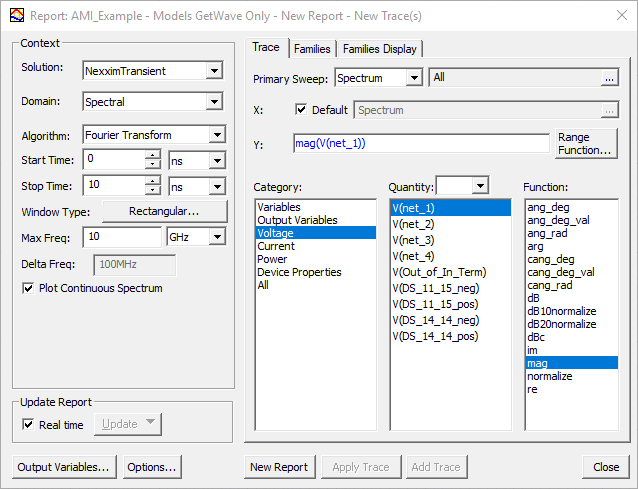
In the Context pane:

• Start Time and Stop Time define the signal duration T₀ = Stop Time - Start Time.
  
  Note: Stop Time and Start Time should lie inside the transient simulation time limits.
• Max Freq sets the maximum frequency for spectral analysis and plotting.
• Delta Freq is automatically supplied as 1/T₀ Hz.
• The Algorithm drop-down menu contains 3 options: Fourier Integration (FI), FFT, and Fourier Transform.

  Fourier Integration and FFT both provide Fourier Series (or Fourier Coefficients) of the transient signal with DFT, where periodicity is implicitly assumed and the period is defined as T₀ = Stop Time - Start Time.

  Fourier Integration computes Fourier series by numerically integrating the input waveform from its transient simulation. The sampled waveform may not be on a set of evenly spaced time points. Fourier Integration is much slower compared with FFT, but it can be more accurate since it preserves the shape of underlying waveform without re-sampling.

  The FFT algorithm re-samples the input waveform by interpolating to evenly spaced time points. It uses the FFTW library that is publicly available and whose computational complexity is

  

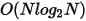
  where N is the sample size after re-sampling and N = 2 *#Harmonics +1, where #Harmonics = Max Freq /Delta Freq.

  Note:

  • Based on the Nyquist-Shannon Theorem or Sampling Theorem, the sampling rate should be at least twice the bandwidth of the signal to avoid aliasing.
  • Spectral plots based on Fourier Integration and FFT are single-sided with magnitudes of non-zero harmonics doubled because the negative frequency components are folded to the positive side.

  Fourier Transform (FT) provides the Fourier transform of a signal defined in [Start Time, Stop Time] by leveraging the FFT algorithm. The Fourier transform of a time limited signal f(t) in [0, T₀] is

  

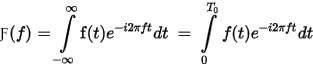
  The Fourier series of a periodic signal that is equal to f(t) in [0, T₀] and with period T₀ is

  

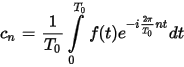
  Hence,

  

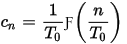
  In other words, the Fourier series of f(t) based on FFT can be multiplied by T₀ in order to get the Fourier Transform of f(t) at sampled frequencies n/T₀.

  Note: Spectral plots based on Fourier Transform only show the positive frequency side.
• The Plot Continuous Spectrum check box provides a continuously plotted spectrum if selected and a discrete spectrum when cleared.
• Window Type determines which window type to apply.

  When applied to transient data, a window type can help resolve closely spaced harmonics and reduce spectral leakage due to the finite nature of the time signal. The following window types are available. (The “t” parameter is normalized time.)

  • Rectangular: 1.0
  • Bartlett (also known as the Parzen or triangular window): 1.0 - t
  • Blackman: 0.42 + 0.5*cos(π*t) + 0.08*cos(2*π*t)
  • Hamming: 0.54 + 0.46*cos(π*frac)
  • Hanning: 0.5 * (1.0 + cos(π*t))
  • Kaiser: BesselI0( KaiserParam * sqrt(1.0 - t*t)) / BesselI0( KaiserParam )
  • Welch: 1.0 - t²
  • Weber: (0.828217*π³*t³ - 1.637363*π²*t² + 0.041186*π*t + 0.99938)
  • Lanzcos: sin(π*t)

  Optionally, click the Adjust Coherent Gain check box to adjust signal levels (based on the window type) as if no window are used. When non-rectangular windows are used, the window automatically changes the power level of the signal. This is known as the “coherent gain” or “processing loss” of the window.

References:

[1] Fredric J. Harris, "From the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform," Proceedings of the IEEE 66, no. 1 (Jan 1978): 51-83, http://web.mit.edu/xiphmont/Public/windows.pdf.

[2] Charan Langton and Victor Levin, "Fourier Transform of continuous and discrete signals," The Intuitive Guide to Fourier Analysis and Spectral Estimation with MATLAB (Mountcastle Academic, 2017), chap. 4, http://complextoreal.com/wp-content/uploads/2012/12/fft4.pdf.

[3] Paul Heckbert, "Fourier Transforms and the Fast Fourier Transform (FFT) Algorithm" (Notes 3 class handout for Computer Graphics 2, 15-463, Carnegie Mellon University, Pittsburgh, PA, Jan 27,1998), http://www.cs.cmu.edu/afs/andrew/scs/cs/15-463/2001/pub/www/notes/fourier/fourier.pdf.

[4] Rolf Isermann and Marco Münchhof, " Spectral Analysis Methods for Periodic and Non-Periodic Signals," Identification of Dynamic Systems (Springer, Berlin, Heidelberg, 2011), chap. 3, https://link.springer.com/chapter/10.1007%2F978-3-540-78879-9_3.

[5] Julius O. Smith III, Mathematics of the Discrete Fourier Transform (DFT) with Audio Applications, 2nd ed. (W3K Publishing, 2007), https://www.dsprelated.com/freebooks/mdft/.