Feed-Forward Equalization
Equalization is one of the principal methods for improving the signal integrity of a channel. Equalization can be applied at the transmitter (Eye Source), the receiver (Eye Probe), or both. The Eye Source provides Feed-Forward Equalization (FFE). The Eye Probe provides Decision-Feedback Equalization (DFE) and Continuous-Time Linear Equalization (CTLE). This topic describes how Nexxim performs driver-side FFE. See Decision Feedback Equalization for details on DFE. See Continuous-Time Linear Equalization for details on CTLE.
Feed-forward equalization (FFE) is an extended form of frequency enhancement. Channels typically attenuate high-frequencies more than low frequencies. FFE adjusts the waveform being injected into the channel to compensate for frequency-dependent losses suffered during propagation.
The basic idea of FFE is to replace a single driver with a series of drivers, each one delayed by a set amount on the previous one. The delay in Nexxim is the unit interval (UI). These drivers are called taps. Each tap drives with a given strength, called the tap weight. The tap weights are set so as to reduce intersymbol interference (ISI).
Calculating the FFE Tap Weights
The algorithm for automatically calculating the tap weights in QuickEye and VerifEye is the Zero-Forcing Equalizer (ZFE). The ZFE algorithm is invoked when the FFE weights are not given but a non-zero number of taps is specified. The algorithm starts with the response to the channel of a rising step function.
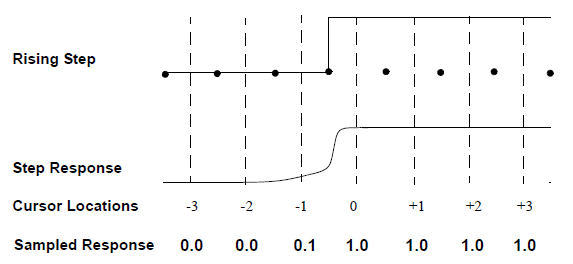
In the preceding figure, the dots on the Rising Step function plot delimit the unit intervals (UIs).
The dotted lines show the time locations of the cursors or sample points for the Step Response. The cursors are at the midpoint of each UI in this example. The numbers under the cursor lines are cursor locations. Location 0 is the main cursor, sampling the response at the center of the pulse. Cursors at locations -1, -2, -3, etc. are precursors, sampling the values of bits that occur earlier in time than the main cursor. Cursors at locations +1, +2, +3, etc. are postcursors, sampling the values of bits that occur later in time than the main cursor. The lowest line in the preceding figure,shows the value of the sampled step response at each cursor.
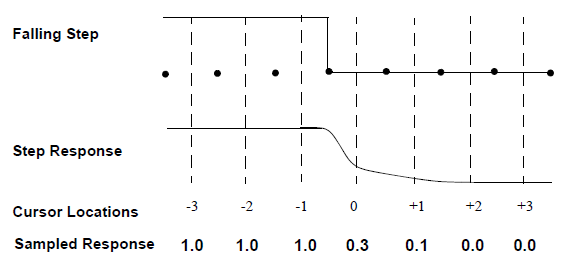
Inverting the rising step response produces the falling step response.
Adding the rising step response to the falling step response shifted one UI simulates the response of the channel to a unit pulse.
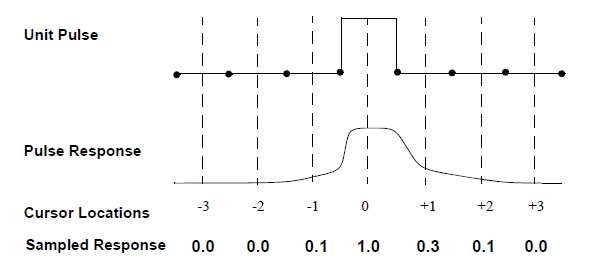
The goal is to make the total response zero at the time points corresponding to the center of the eye for ISI for a number of cursors in the pulse response equal to the number of FFE taps specified. The FFE setup window lets you specify how many taps to use and which cursor locations to equalize. Each sampled response is replaced by a weighted sum of the neighboring responses.
For example, a three-tap FFE with starting location -1 equalizes the main cursor, one precursor, and one postcursor. The equation for the weighted sum looks something like Equation 1:
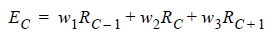
(1)
Where:
EC is the equalized value of the response at cursor C.
w1, w2, and w3 are the weights associated with the three taps.
RX is the sampled value of the response at the cursor locations X = C-1, C, and C+1.
Applying this formula over a number of cursors and setting each weighted sum to the corresponding value in the unit pulse produces a system of equations. Using the pulse response in the preceding figure, here are the equations for a three-tap FFE with one precursor (C = -1), the main cursor (C = 0) and one postcursor (C = +1).
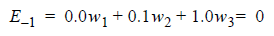
(2)
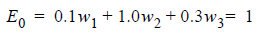
(3)
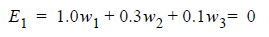
(4)
The sampled responses are known, and all other cursor values are forced to be zero. Solving for the tap weights yields w1 = -0.308, w2 = 1.063, and w3 = -0.106.
- QuickEye and VerifEye normalize the automatically calculated tap weights such that the sum of all weights is 1.0. No calculation is done in this example.
- The cursor locations in principle extend infinitely in both directions, and always exceed the number of taps. The response of cursors outside the tapped region can limit the accuracy of the tap weight calculations. Nexxim applies an error-minimizing algorithm to correct for this source of error. This calculation is not shown in this example.
Applying the FFE Tap Weights to Generate the Output Voltages
To generate the output, QuickEye and VerifEye apply the tap weights are applied to the step response Vs(t) calculated using the transient analysis engine of the Circuit solver.
Begin with the default operation, no equalization. QuickEye and VerifEye apply the step response to the rising and falling edges in the bit pattern.
Here are some terms to be used in the formulas:
The step response is Vs(t) .
The subscript i references the cursor locations
where bits are evaluated, 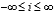 .
.
bi is the value (0 or 1) of the bit at cursor location i.
The step response is applied only at transitions. Function is defined a to be the exclusive-OR of the current bit and its immediate predecessor:
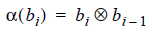
Function a is 1 when the bits differ, indicating that a transition has occurred. Function a is 0 for non-transitions.
When the current bit is a one, the transition is a rising edge and the sign of the step response is positive. When the current bit is a zero, the transition is a falling edge and the sign of the step response is negative. Function is defined b(bi) to set the sign of the adjustment based on the bit value (0 or 1) of bi.
b(0) = -1, b(1)= +1
With this notation, the formula for the unequalized output voltage is expressed at time t as follows:
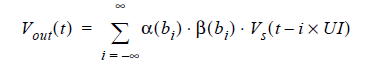
(5)
Now add N taps of FFE, indexed with variable
j, which is swept on the Starting Location specified in the
GUI, 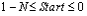 , to the
Ending Location,
, to the
Ending Location, 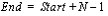 .
The series of tap locations must always include location 0.
.
The series of tap locations must always include location 0.
The tap weights Wj are the ones calculated earlier.
Using this notation, express the formula for the voltage output adjusted by FFE as follows:
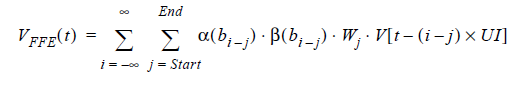
(6)
FFE in the Frequency Domain
Channel attenuation is equivalent to adding a low-pass filter. To compensate, the FFE acts as a high-pass filter in the frequency domain.
The frequency response H(s) is the Laplace transform of the time domain pulse response R(t). The frequency response of an N-tap equalized signal H(s)FFE can be calculated on the unequalized frequency response H(s), the tap weights Wj, and the time delays Tj.
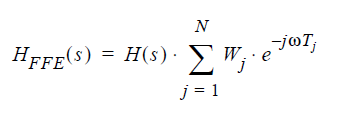
(7)
The frequency response on the typical FFE is that of a high-pass filter.
FFE Examples
Figures 1 and 2 show Quick Eye analyses without equalization and with FFE.
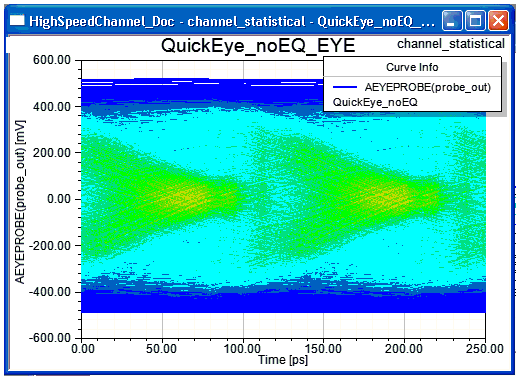
Figure 1. Quick Eye analysis of a high-speed channel with no equalization.
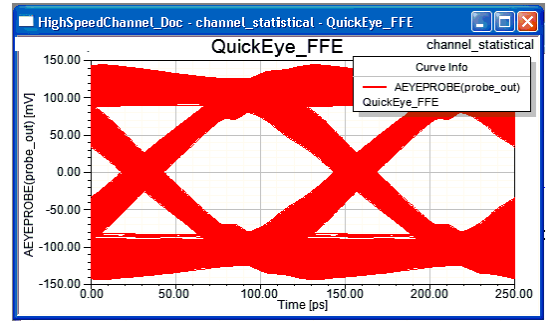
Figure 2. Quick Eye analysis of the high-speed channel with 4-tap FFE. The tap coefficients automatically calculated by the Circuit solver are (0.5797, -0.3481, 0.0386, and -0.0335).
Figures 3 and 4 show VerifEye analyses without equalization and with Feed-Forward Equalization.
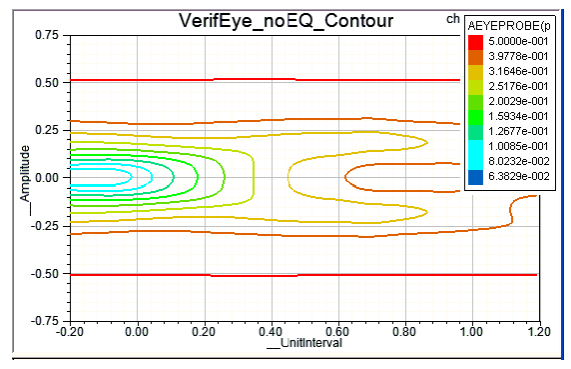
Figure 3. VerifEye analysis of a high-speed channel with no equalization.
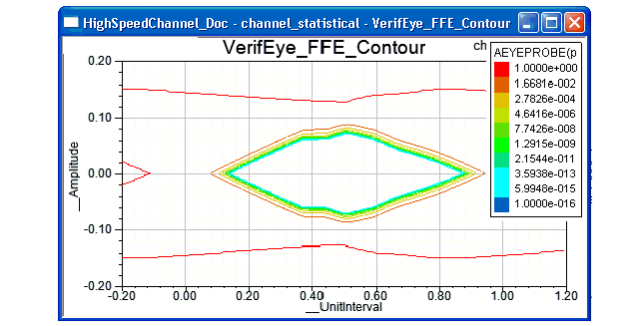
Figure 4. VerifEye analysis of the high-speed channel with 4-tap FFE. The tap coefficients automatically calculated by the Circuit solver are (0.59792, -0.3481, 0.03863, and -0.03355).
Feed-forward equalization is set up in the Eye Source, using the FFE_TAPS, FFE_LOCS, FFE_WEIGHTS, NORMALIZE_FFE_WEIGHTS, and FFE_COMPUTE_PROBE parameters.
