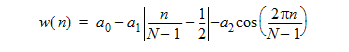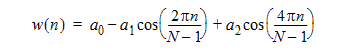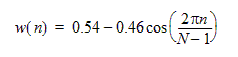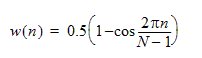TDR Windowing Functions

Windowing functions cause the FFT of the signal to have non-zero values away from w. Each window function trades off the ability to resolve comparable signals and frequencies versus the ability to resolve signals of different strengths and frequencies. The window type list includes:

Window Function	Preferred Use
Rectangular	A low dynamic range function offering good resolution for signals of comparable strength. Poor when signals have very different amplitudes. w(n)=1.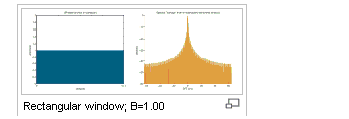
Bartlett	A high dynamic range function, with lower resolution, designed for wide band applications. where a₀=0.62; a₁=0.48; a₂=0.38
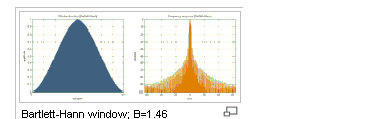
Blackman	A high dynamic range function, with lower resolution, designed for wide band applications. where a₀ =(1-a)/2; a₁=1/2; a₂=a/2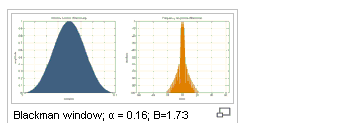
Hamming	A moderate dynamic range function, designed for narrow band applications. It minimizes the maximum sidelobe.
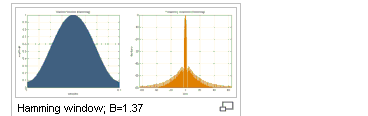
Hanning (default)	A moderate dynamic range function, designed for narrow band applications.
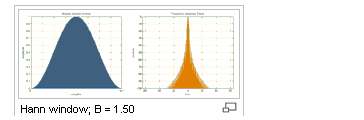
Kaiser	Selecting the Kaiser plot also enables a field to specify an associated Kaiser parameter. The larger the Kaiser parameter, the wider the window. The parameter controls the trade off between width of the central lobe and the area of the side lobes.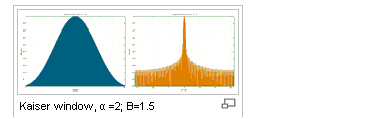
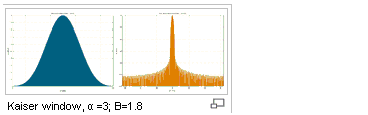
Welch	This approach applies a parabola-shaped window to the frequency domain data. It is based on the Bartlett method but splits the signal into overlapping segments, which are then windowed. The intent is to balance the influence of data in the center of the function.

You can use the Save as Default to set the current values as a default, and the Use Defaults