Eval Command

The Eval command finalizes computations and converts the text-string indicating the computation being performed to an actual numerical value. This command numerically evaluates and displays the results of calculator operations such as integrations, maximum or minimum field computations, field values at points, and so forth. For this command to work properly, the stack entry must be reduced to a single-value entry which can be a scalar, complex, or vector (real or complex). The quantity to be evaluated must be in the top register. The Eval command computes the numerical results of the operation, which replace the contents of the register. Units of the numerical value are not provided.

For a calculator expression that evaluates to a single value, the Eval command offers a quicker way to obtaining the final numerical result than defining a named expression and then trying to plot/tabulate it in the reporter. But for many expressions that don't evaluate to single values, such as the wave impedance along a line mentioned earlier, Eval command does not apply. As such, use of named expression and the Report Editor will be the only option.

Evaluate the expression for voltage along a line shows the definition of an expression for the voltage between two conductors by integrating the electric field along a line using the recipe given for Calculating the Current along a Wire or Trace. Then, by clicking the Evaluate command in the Output column, we obtain the numerical value for the voltage as shown in the top of the stack. It can then be either written down or copied/pasted to other programs.

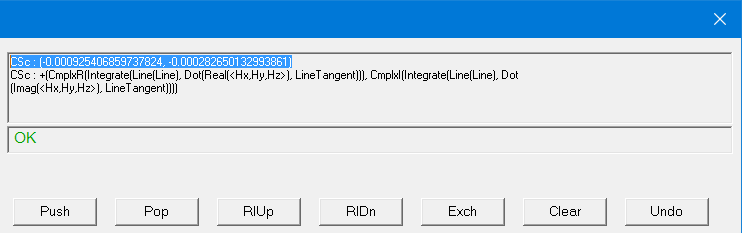
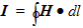
Because H and I are complex quantities, you will need to evaluate the real part of H to obtain the real part of I, then evaluate the imaginary part of H to obtain the imaginary part of I. To do this:

1. Load H into the calculator using the Qty command.
2. Take the real part of H using the Cmplx/Real command.
3. Load the rectangular loop using the Geom/Line command. Create the loop, a closed polyline, to integrate over.
4. Click Tangent to get the component of H along the line.
5. Take the integral around the loop using the command.
6. Click Eval to evaluate the integral. The real part of I appears in the top register.
7. Repeat this process using the imaginary part of H (found with the Cmplx/Imag command) to obtain the imaginary part of I.