Calculating the Peak Electrical Energy in a Volume
Description
This recipe permits you to calculate the peak electrical energy in a volume object. The solution is achieved by integrating EE within the volume.
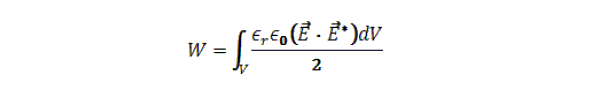
where V is the volume.
Usage Examples
This calculation could be used to determine the average total energy with respect to time in a terminating resonant cavity. (In a sealed, one-port structure at resonance, energy is converted back and forth between the electrical and magnetic fields, but maintains the same total quantity; therefore the peak electrical energy is equal to the average total energy.)
Prerequisites
The volume object which the integration is to be performed must exist before the computation can be completed. If the volume for integration consists of the volume of several drawing objects, you must create a single list entry representing their combined volumes using Modeler>Lis>Create>Object List.
|
Calculator Operation |
Resulting Stack Display (top entry only unless noted) |
|
Quantity>E |
CVc : <Ex, Ey, Ez> |
|
Complex>Conj |
CVc : Conj(<Ex, Ey, Ez>) |
|
Quantity>E |
CVc : <Ex, Ey, Ez> |
|
Dot |
CSc : Dot(Conj(<Ex, Ey, Ez>), <Ex... |
|
Complex>Real |
Scl : Real(Dot(Conj(<Ex, Ey, Ez>), ... (note: the dot product of the E with its conjugate should lead to a real quantity, but the calculator still assume as complex) |
|
Geometry>Volume...>{select volume} |
Vol : Volume(box1) (above is example, user entry may differ) |
|
|
Scl : Integrate(Volume(... |
|
Eval |
Scl : {numerical quantity} |
|
Constant>Epsi0 |
Scl : 8.854187817E-012 |
|
Number>Scalar>{enter r for volume} |
Scl : {numerical quantity} |
|
* |
Scl : {numerical quantity} (stack entry is volume ) |
|
Number>Scalar>0.5 |
Scl : 0.5 |
|
* |
Scl : {numerical quantity} |
|
* |
Scl : {numerical quantity} above is electrical energy in joules |