Multi-Objective Genetic Algorithm (MOGA)

The Multi-Objective Genetic Algorithm (MOGA) used in GDO is a hybrid variant of the popular NSGA-II (Non-dominated Sorted Genetic Algorithm-II) based on controlled elitism concepts. It supports all types of input parameters. The Pareto ranking scheme is done by a fast, non-dominated sorting method that is an order of magnitude faster than traditional Pareto ranking methods. The constraint handling uses the same non-dominance principle as the objectives. Therefore, penalty functions and Lagrange multipliers are not needed. This also ensures that the feasible solutions are always ranked higher than the infeasible solutions.

The first Pareto front solutions are archived in a separate sample set internally and are distinct from the evolving sample set. This ensures minimal disruption of Pareto front patterns already available from earlier iterations. You can control the selection pressure (and, consequently, the elitism of the process) to avoid premature convergence by altering the Maximum Allowable Pareto Percentage property. For more information about this and other MOGA properties, see Setup Multi-Objective Genetic Algorithm.

MOGA Workflow

The MOGO workflow follows:

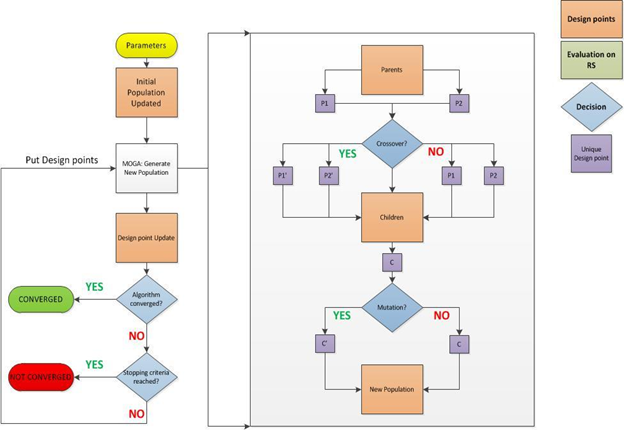
MOGA Steps

1. First Population of MOGA

   The initial population is used to run MOGA.

2. MOGA Generates a New Population

   MOGA is run and generates a new population via cross-over and mutation. After the first iteration, each population is run when it reaches the number of samples defined by the Number of Samples Per Iteration property. For details, see MOGA Steps to Generate  New Population below.

3. Design Point Update

   The design points in the new population are updated.

4. Convergence Validation

   The optimization is validated for convergence.

   • Yes: Optimization Converged

     MOGA converges when the Maximum Allowable Pareto Percentage or the Convergence Stability Percentage has been reached.

   • No: Optimization Not Converged

     If the optimization is not converged, the process continues to the next step.

5. Stopping Criteria Validation

   If the optimization has not converged, it is validated for fulfillment of stopping criteria.

   • Yes: Stopping Criteria Met

     When the Maximum Number of Iterations criterion is met, the process is stopped without having reached convergence.

   • No: Stopping Criteria Not Met

     If the stopping criteria have not been met, MOGA is run again to generate a new population (return to Step 2).

6. Conclusion

   Steps 2 through 5 are repeated in sequence until the optimization has converged or the stopping criteria have been met. When either of these things occurs, the optimization concludes.

MOGA Steps to Generate a New Population

The process MOGA uses to generate a new population has two main steps: Cross-over and Mutation.

1. Cross-over

   Cross-over combines (mates) two chromosomes (parents) to produce a new chromosome (offspring). The idea behind cross-over is that the new chromosome can be better than both of the parents if it takes the best characteristics from each of the parents. Cross-over occurs during evolution according to a user-definable cross-over probability.

   • Cross-over for Continuous Parameters

     A cross-over operator that linearly combines two parent chromosome vectors to produce two new offspring according to the following equations:

     

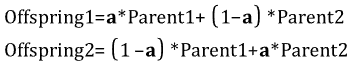
     Consider the following two parents (each consisting of four floating genes), which have been selected for cross-over:

     

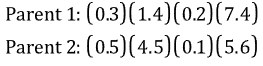
     If a = 0.7, the following two offspring would be produced:

     

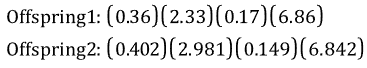
   • Cross-over for Discrete Parameters and Continuous Parameters with Manufacturable Values

   Each discrete parameter or continuous parameter with manufacturable values is represented by a binary chain corresponding to the number of levels. For example, a parameter with two values (levels) is encoded to one bit, a parameter with seven values is encoded to three bits, and an -bits chain represents a parameter with values.

   The concatenation of these chains forms the chromosome, which crosses over with another chromosome.

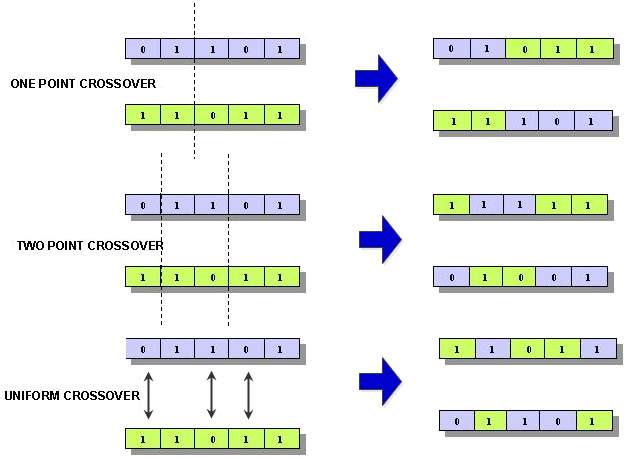
   Three different kinds of cross-over are available:

   • One-Point

     A one-point cross-over operator that randomly selects a cross-over point within a chromosome then interchanges the two parent chromosomes at this point to produce two new offspring.

   • Two-Point

     A two-point cross-over operator randomly selects two cross-over points within a chromosome then interchanges the two parent chromosomes between these points to produce two new offspring.

   • Uniform

     A uniform cross-over operator decides (with some probability, which is known as the "mixing ratio") which parent contributes each of the gene values in the offspring chromosomes. This allows the parent chromosomes to be mixed at the gene level rather than the segment level (as with one and two-point cross-over). For some problems, this additional flexibility outweighs the disadvantage of destroying building blocks.

   

2. Mutation

   Mutation alters one or more gene values in a chromosome from its initial state. This can result in entirely new gene values being added to the gene pool. With these new gene values, the genetic algorithm might be able to arrive at a better solution than was previously possible. Mutation is an important part of the genetic search, as it helps to prevent the population from stagnating at any local optima. Mutation occurs during evolution according to a user-defined mutation probability.

   • Mutation for Continuous Parameters

     For continuous parameters, a polynomial mutation operator is applied to implement mutation.

     

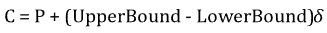
     where C is the child, P is the parent, and δ is a small variation calculated from a polynomial distribution.

   • Mutation for Discrete Parameters and Continuous Parameters with Manufacturable Values

     For discrete parameters or continuous parameters with manufacturable values, a mutation operator simply inverts the value of the chosen gene (0 goes to 1 and 1 goes to 0) with a probability of 0.5. This mutation operator can only be used for binary genes. The concatenation of these chains forms the chromosome, which crosses over with another chromosome.