Mixed-Integer Sequential Quadratic Programming
Mixed-Integer Sequential Quadratic Programming (MISQP) is a mathematical optimization algorithm as developed by Oliver Exler, Thomas Lehmann and Klaus Schittkowski (NLPQL). This method solves Mixed-Integer Non-Linear Programming (MINLP) of the form:
Minimize:
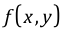
Subject to:
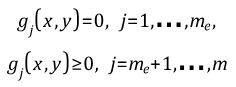
Where:
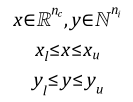
The symbols and denote the vectors of the continuous and integer variables, respectively. It is assumed that problem functions and are continuously differentiable subject to all . It is not assumed that integer variables can be relaxed. In other words, problem functions are evaluated only at integer points and never at any fractional values in between.
MISQP solves MINLP by a modified sequential quadratic programming (SQP) method. After linearizing constraints and constructing a quadratic approximation of the Lagrangian function, mixed-integer quadratic programs are successively generated and solved by an efficient branch-and-cut method. The algorithm is stabilized by a trust region method as originally proposed by Yuan for continuous programs. Second order corrections are retained. The Hessian of the Lagrangian function is approximated by BFGS updates subject to the continuous and integer variables. MISQP is able to solve also non-convex nonlinear mixed-integer programs.
