Convergence Rate % and Initial Finite Difference Delta % in NLPQL and MISQP

Convergence Rate % and Initial Finite Difference Delta % in NLPQ and MISQP

Typically, the use of Nonlinear Programming by Quadratic Lagrangian (NLPQL) or Mixed-Integer Sequential Quadratic Programming (MISQP) optimizers is suggested for continuous problems when there is only one objective function. The problem might or might not be constrained and must be analytic. This means that the problem must be defined only by continuous input parameters and that the objective functions and constraints should not exhibit sudden "jumps" in their domain.

The main difference between these algorithms and Multi-Objective Genetic Algorithm (MOGA) is that MOGA is designed to work with multiple objectives and does not require full continuity of the output parameters. However, for continuous single objective problems, the use of NLPQL or MISQP gives greater accuracy of the solution as gradient information and line search methods are used in the optimization iterations. MOGA is a global optimizer designed to avoid local optima traps, while NLPQL and MISQP are local optimizers designed for accuracy.

For NLPQL and MISQP, the default convergence rate, which is specified by the Allowable Convergence (%) property, is set to 0.1% for a Direct Optimization system. The maximum value for this property is 100%. This is computed based on the (normalized) Karush-Kuhn-Tucker (KKT) condition. This implies that the fastest convergence rate of the gradients or the functions (objective function and constraint) determine the termination of the algorithm.

The default convergence rate is used in conjunction with the initial finite difference delta percentage value, which is specified by the Initial Finite Difference Delta (%) advanced property. This property defaults to 1% for a Direct Optimization system. You use this property to specify a percentage of the variation between design points to ensure that the Delta use in the calculation of finite differences is large enough to be seen over simulation noise. The specified percentage is defined as a relative gradient perturbation between design points.

The advantage of this approach is that for large problems, it is possible to get a near-optimal feasible solution quickly without being trapped into a series of iterations involving small solution steps near the optima. To work most effectively with NLPQL and MISQP, keep the following guidelines in mind:

If the Initial Finite Difference Delta (%) is greater than the Allowable Convergence (%), the relative gradient perturbation gets iteratively smaller, until it matches the allowable convergence rate. At this point, the relative gradient value stays the same through the rest of the analysis.
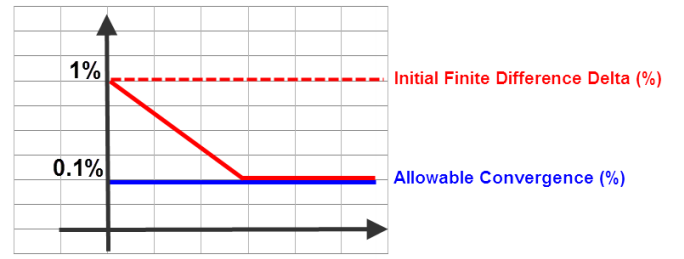
If the Initial Finite Difference Delta (%) is less than or equal to the Allowable Convergence (%), the current relative gradient step remains constant through the rest of the analysis.
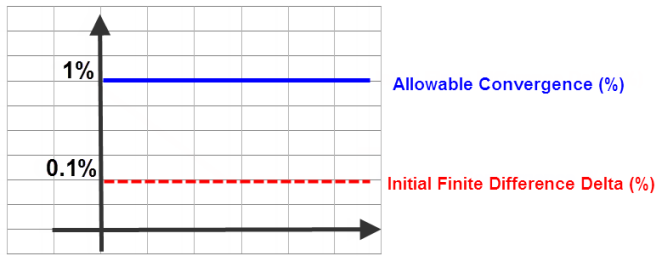
Both the Initial Finite Difference Delta (%) and Allowable Convergence (%) should be higher than the magnitude of the noise in your simulation.

When setting the values for these properties, you have the usual trade-offs between speed and accuracy. Smaller values result in more convergence iterations and a more accurate (but slower) solution, while larger values result in fewer convergence iterations and a less accurate (but faster) solution. At the same time, however, you must be aware of the amount of noise in your model. For the input variable variations to be visible in the output variables, both values must be greater than the magnitude of the simulation's noise.

In general, default values for Initial Finite Difference Delta (%) and Allowable Convergence (%) cover the majority of optimization problems. For example, if you know that the noise magnitude in your direct optimization problem is 0.0001, then the default values (Allowable Convergence (%) = 0.001 and Initial Finite Difference Delta (%) = 0.01) are good.

When the defaults are not a good match for your problem, of course, you can adjust the values to better suit your model and your simulation needs. If you require a more numerically accurate solution, you can set the convergence rate to as low as 1.0E-10% and then set the Initial Finite Difference Delta (%) accordingly.